欢迎访问TK Xiong Blog. Code & Algorithm.
启发式策略的搜索算法
摘要:
在数据结构的学习中,常用的搜索算法有深度优先(DFS)和广度优先(BFS)两种,但是它们都有一定的缺陷,当目标状态空间特别大的时候,因为要穷举到所有的情况,所以执行效率太低,当数据量较大时,建议采用一种特殊的策略进行搜索,这种策略成为启发式策略。
关键词:
启发式策略,启发式搜素算法,A*算法,搜索算法
1. 引言
状态空间搜索:在介绍启发式策略之前,我们先来看看什么叫做状态空间搜索。
百度百科的定义是这样的: 状态空间搜索就是将问题求解过程表现为从初始状态开始到目标状态的这样一个寻找路径的过程。
即:我们将我们在搜索的过程中所碰到的每一种情况定义为一种状态,从一种状态可以到达另一种状态,从初始状态到我们需求的目标状态有一个转化的过程,将这个过程定义为一条路径,我们寻找这个路径的过程,称之为状态空间搜索。
2. 启发式策略介绍
- 启发信息是什么,在智能搜索中,常把搜索中出现的类似于问题的状态条件、性质、发展动态,解的过程特性、结构特性,问题求解的技巧性规则等,称之为搜索的启发信息。
- 启发式策略是什么,启发式策略是指人们在推理任务中,往往采用的一些推理规则;这些规则不一定遵循标准逻辑规范,但在生活情景中也能帮助人们作出快速的、基本有效的推断。
算法中的启发式策略则是:利用与问题解有关的启发信息来作引导的搜索策略。
例如:方向的限定,优先向目标状态的方向进行搜索而不是往与其相反的方向进行搜索。状态的限定,优先选择开销较小,获利较大的等等…
- 估价函数 F(x) = G(x) + H(x)
F(x) : 从Ss经过结点x到达目标节点Se 的最优路径的代价估计值,作用是估价Open表中各节点的重要性,决定Open表的次序。
G(x) : 从Ss到节点x已经实际付出的代价。指出了搜索的横向趋势、完备性好,但效率差。
H(x) : 从节点x到达目标节点Se的最优路径的估计代价,称为启发函数。
在人工智能问题的求解中,我们往往就是需要去找到一个好的启发函数,使我们的代码显得更加地智能化。
估价值 H(n) <= n到目标节点的距离的实际值 时,搜索的点数较多,搜索范围较大,效率较低。但是这样可以得到最优解。
如果 H(n) = n到目标节点的距离的实际值 时,搜索将恰好沿着最短路进行,这样搜索的效率是最高的。
估价值 H(n) > n到目标节点的距离的实际值 时,搜素的点数较少,搜索的范围较小,效率较高,但是不能保证得到最优解。
2. 启发式搜索的应用实例
3.1八数码
题目链接:
杭电:http://acm.hdu.edu.cn/showproblem.php?pid=1043
北大:http://poj.org/problem?id=1077
在Goodness大牛的博客里写出了八数码的这个问题的八种解决思路。
我这里考虑学习A*+哈希+简单估价函数 和 A*+哈希+曼哈顿距离 这两种方法来解决这个问题。
A*+哈希+简单估价函数
A*:用搜索的深度作为G(n)(实际已经付出的代价),启发函数H(n)可以用两种状态 它们不相同数字的数目,同时需要注意以下两点:
1.H(n)>H’(n) , H’(n)为从当前节点到目标状态结点的实际的最优代价值。
2.每次扩展的结点的f值 大于等于 父结点的f值。
哈希:这里的哈希需要使用到排列的方法,叫做康托展开。可以在本人的Blog里找到这个问题的思想以及方法:http://blog.tk-xiong.com/archives/62
我们可以把八数码的九个数分别理解为 1 2 3 4 5 6 7 8 9,其中9代表着空。
那么![]() 这样的状态可以写成 1 2 3 9 4 6 7 5 8 …使用康托展开计算的哈希值为:
这样的状态可以写成 1 2 3 9 4 6 7 5 8 …使用康托展开计算的哈希值为:
0*0! + 0*1! + 0*2! + 5*3! + 0*4! + 1*5! + 1*6! + 0*7! + 0*8! < 9!
我们知道,计算出来的哈希值,是在 0(012345678) 到 9!-1= 362879(876543210)这两个数
据之间的。
截图: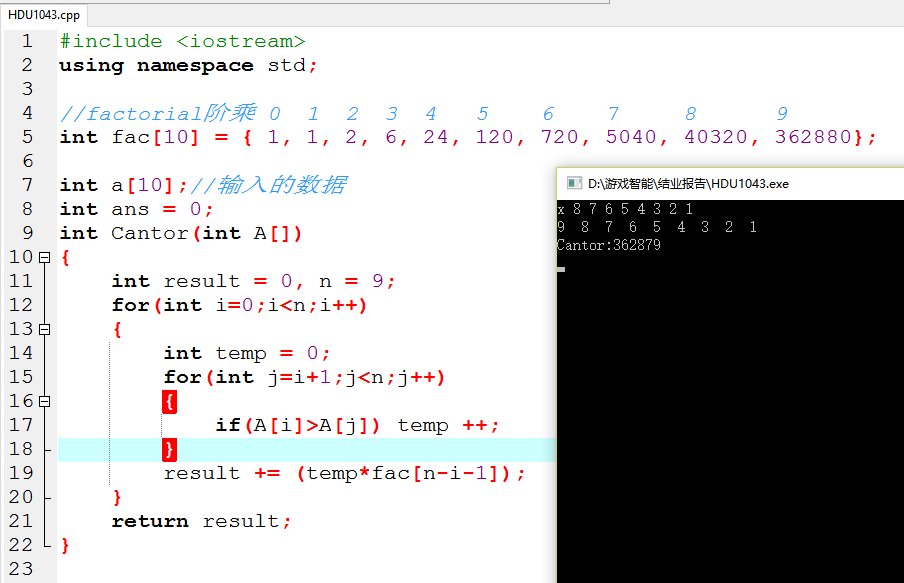

简单估价函数:即用 两种状态 它们不相同数字的数目,比如:在问题描述里面给出的(123946758),它和我们需要得到的最终状态(123456789)的不相同的数字有四组,分别是第四个,第五个,第八个和第九个.这样它的估价函数的值就应该是 4.
截图: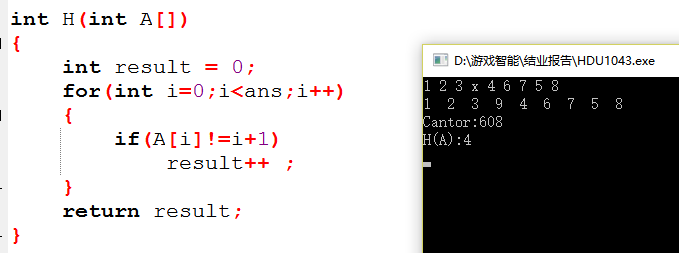
逆序对判断:
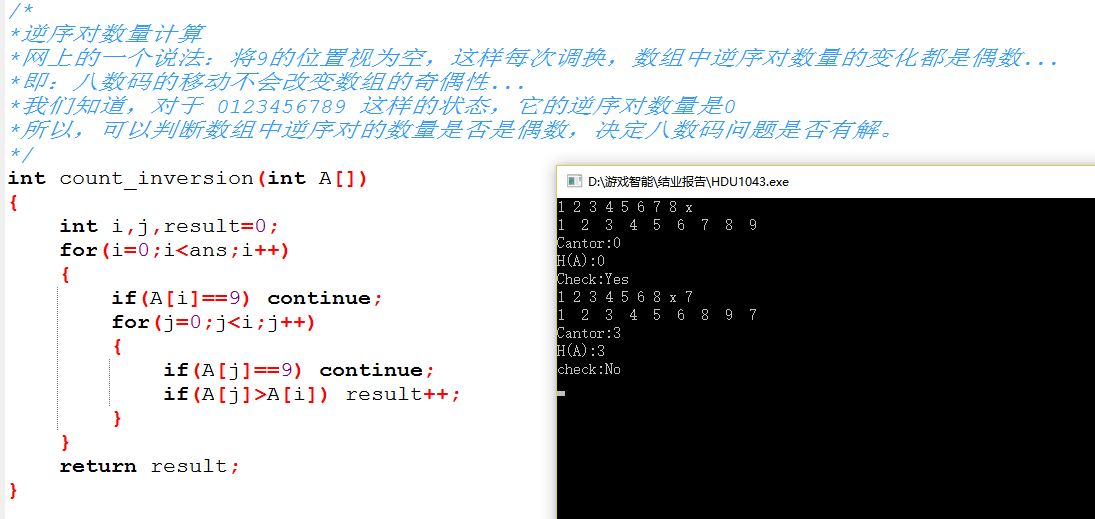
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 |
#include <iostream> #include <queue> #include <algorithm> #include <vector> #include <cstdio> #include <cstring> using namespace std; const int Size_N = 400000; //factorial阶乘 0 1 2 3 4 5 6 7 8 9 int fac[15] = { 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; int a[10]; //输入的数据 int ans = 0; //数据的个数 int Start,End; //记录开始节点和结束节点的哈希值 bool visit[Size_N]; //某个节点是否被访问过 char dir[Size_N]; //行走的方向 int pre[Size_N]; //记录当前节点的前一个节点的Hash值 struct node { int m_a[10]; //当前节点对应的a的值 int m_hash; //节点的Hash值 int m_x; //x(空格)的位置 int m_f; //F() int m_g; //G() bool operator <(const node &temp)const { return temp.m_f < m_f; } }; //康托展开函数,计算哈希值 inline int Cantor(int A[]) { int result = 0; for(int i=0;i<ans;i++) { int temp = 0; for(int j=i+1;j<ans;j++) { if(A[i]>A[j]) temp ++; } result += (temp*fac[ans-i-1]); } return result; } //简单估价函数H() inline int H(int A[]) { int result = 0; for(int i=0;i<ans;i++) { if(A[i]!=i+1) result++ ; } return result; } /* *逆序对数量计算 *网上的一个说法:将9的位置视为空,这样每次调换,数组中逆序对数量的变化都是偶数... *即:八数码的移动不会改变数组的奇偶性... *我们知道,对于 0123456789 这样的状态,它的逆序对数量是0 *所以,可以判断数组中逆序对的数量%2是否是0,决定八数码问题是否有解。 */ int count_inversion(int A[]) { int i,j,result=0; for(i=0;i<ans;i++) { if(A[i]==9) continue; for(j=0;j<i;j++) { if(A[j]==9) continue; if(A[j]>A[i]) result++; } } return result; } //广度搜索 void bfs() { int hash; //计算的Hash值 priority_queue<node>q; //优先队列,确定搜索顺序 node current,next; //当前节点 和 下一个节点 Start = Cantor(a); //开始节点的Hash值 if(Start==End) return; //如果头等于尾 即不需要寻找 current.m_hash=Start; //当前节点的Hash值 current.m_g=0; //当前节点的G()=0 current.m_f=H(a); //当前节点的F()=0+H(a); for(int i=0;i<ans;i++) //当前节点的数据,同时记录X的位置 { current.m_a[i]=a[i]; if(a[i]==9) current.m_x=i; } visit[Start] = true; //首节点已访问。 q.push(current); //将首节点加入到队列中 while(!q.empty()) { current = q.top(); //获取第一个元素的值 q.pop(); //首元素出队 if((current.m_x)/3!=0) //向上 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x-3; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='u'; //Up if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if((current.m_x)/3!=2) //向下 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x+3; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='d'; //Down if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if(current.m_x%3!=0) //向左 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x-1; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='l'; //Left if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if(current.m_x%3!=2) //向右 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x+1; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='r'; //Right if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } } } int main() { char str[1000]; while(gets(str)) { memset(visit,0,sizeof(visit)); ans = 0; //处理数据 在ASCII 中,0表示换行符 for(int i=0;str[i]!='\0';i++) if(str[i] == 'x') a[ans++]=9;//9表示空 else if(str[i] != ' ') a[ans++]=str[i]-'0';//数字 //判断逆序对,如果是1(奇数),说明无解 if(count_inversion(a)%2) { cout << "unsolvable" << endl; continue; } End=0; //结束节点的Hash值为0 bfs(); //对数组a进行广度搜索(采用启发式策略) int j=0; while(End!=Start)//从终点开始搜索前一个结点,直到找到首节点 { str[j++] = dir[End]; //记录步数和方向 End=pre[End]; } for(int i=j-1;i>=0;i--) //输出结果 cout << str[i]; cout << endl; } return 0; } |
运行截图:


分别是HDU(上面的) 和 PKU(下面的)运行结果的截图。
可以看到,HDU使用了多组测试数据,所以计算时间较长,在G++运行模式下,3800MS(3.8秒的时间通过),在C++运行模式下超过了规定时间。
在PKU中,应该是采用了单组数据,G++运行模式下,大概110MS(0.11秒)可以通过,在C++运行模式下,266MS(0.26秒)可以通过。
可以知道,这样的代码还是需要改进的。
对于A*算法,如果要优化,最好的就是启发函数的设计。
A*+哈希+曼哈顿距离
A* 和 Hash 在前面已经介绍就不再讲解。
曼哈顿距离:两个点在标准坐标系上的绝对轴距总和。
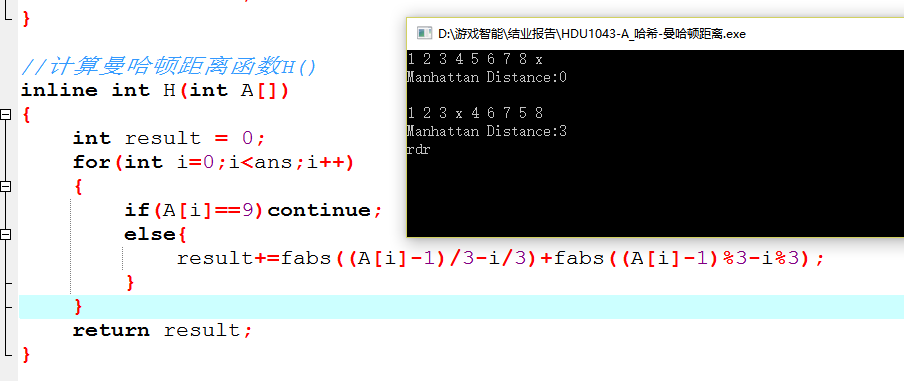
在问题描述里面给出的![]() (123946758),它和我们需要得到的最终状态(123456789)的不相同的数字有四组,分别是 4 5 8这四个数字。它们与它们本应该在的位置的曼哈顿距离分别是1 1 1,所以它计算出的H(A) = 3;
(123946758),它和我们需要得到的最终状态(123456789)的不相同的数字有四组,分别是 4 5 8这四个数字。它们与它们本应该在的位置的曼哈顿距离分别是1 1 1,所以它计算出的H(A) = 3;
所以可以修改H()函数,使用曼哈顿距离作为我们的估价函数.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 |
#include <iostream> #include <queue> #include <algorithm> #include <vector> #include <cstdio> #include <cstring> #include <cmath> using namespace std; const int Size_N = 400000; //factorial阶乘 0 1 2 3 4 5 6 7 8 9 int fac[15] = { 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; int a[10]; //输入的数据 int ans = 0; //数据的个数 int Start,End; //记录开始节点和结束节点的哈希值 bool visit[Size_N]; //某个节点是否被访问过 char dir[Size_N]; //行走的方向 int pre[Size_N]; //记录当前节点的前一个节点的Hash值 struct node { int m_a[10]; //当前节点对应的a的值 int m_hash; //节点的Hash值 int m_x; //x(空格)的位置 int m_f; //F() int m_g; //G() bool operator <(const node &temp)const { return temp.m_f < m_f; } }; //康托展开函数,计算哈希值 inline int Cantor(int A[]) { int result = 0; for(int i=0;i<ans;i++) { int temp = 0; for(int j=i+1;j<ans;j++) { if(A[i]>A[j]) temp ++; } result += (temp*fac[ans-i-1]); } return result; } //计算曼哈顿距离函数H() inline int H(int A[]) { int result = 0; for(int i=0;i<ans;i++) { if(A[i]==9)continue; else{ result+=abs((A[i]-1)/3-i/3)+abs((A[i]-1)%3-i%3); } } return result; } /* *逆序对数量计算 *网上的一个说法:将9的位置视为空,这样每次调换,数组中逆序对数量的变化都是偶数... *即:八数码的移动不会改变数组的奇偶性... *我们知道,对于 0123456789 这样的状态,它的逆序对数量是0 *所以,可以判断数组中逆序对的数量%2是否是0,决定八数码问题是否有解。 */ int count_inversion(int A[]) { int i,j,result=0; for(i=0;i<ans;i++) { if(A[i]==9) continue; for(j=0;j<i;j++) { if(A[j]==9) continue; if(A[j]>A[i]) result++; } } return result; } //广度搜索 void bfs() { int hash; //计算的Hash值 priority_queue<node>q; //优先队列,确定搜索顺序 node current,next; //当前节点 和 下一个节点 Start = Cantor(a); //开始节点的Hash值 if(Start==End) return; //如果头等于尾 即不需要寻找 current.m_hash=Start; //当前节点的Hash值 current.m_g=0; //当前节点的G()=0 current.m_f=H(a); //当前节点的F()=0+H(a); for(int i=0;i<ans;i++) //当前节点的数据,同时记录X的位置 { current.m_a[i]=a[i]; if(a[i]==9) current.m_x=i; } visit[Start] = true; //首节点已访问。 q.push(current); //将首节点加入到队列中 while(!q.empty()) { current = q.top(); //获取第一个元素的值 q.pop(); //首元素出队 if((current.m_x)/3!=0) //向上 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x-3; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='u'; //Up if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if((current.m_x)/3!=2) //向下 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x+3; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='d'; //Down if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if(current.m_x%3!=0) //向左 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x-1; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='l'; //Left if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } if(current.m_x%3!=2) //向右 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x=current.m_x+1; //然后对下一个节点的值进行修改 next.m_a[current.m_x] = next.m_a[next.m_x];//和空格交换值 next.m_a[next.m_x]=9; hash=Cantor(next.m_a); //计算下一个节点的哈希值 if(!visit[hash]) //如果下一个节点没有访问过 { //就访问下一个节点 visit[hash]=1; //设置节点已访问 next.m_g++; //实际付出的代价+1 next.m_f=next.m_g+H(next.m_a); //F() = G() + H() next.m_hash=hash; //记录当前节点的Hash值 pre[hash]=current.m_hash; //记录前一个节点的Hash值 dir[hash]='r'; //Right if(hash==End) return; //判断是否结束 q.push(next); //将当前节点加入队列中 } } } } int main() { char str[1000]; while(gets(str)) { memset(visit,0,sizeof(visit)); ans = 0; //处理数据 在ASCII 中,0表示换行符 for(int i=0;str[i]!='\0';i++) if(str[i] == 'x') a[ans++]=9;//9表示空 else if(str[i] != ' ') a[ans++]=str[i]-'0';//数字 //判断逆序对,如果是1(奇数),说明无解 if(count_inversion(a)%2) { cout << "unsolvable" << endl; continue; } End=0; //结束节点的Hash值为0 bfs(); //对数组a进行广度搜索(采用启发式策略) int j=0; while(End!=Start)//从终点开始搜索前一个结点,直到找到首节点 { str[j++] = dir[End]; //记录步数和方向 End=pre[End]; } for(int i=j-1;i>=0;i--) //输出结果 cout << str[i]; cout << endl; } return 0; } |
运行截图:


可以看到,上面的截图HDU的运行时间,相比之前的简单估价函数快了7倍.
而PKU的可以看到,单次运行时间,最快能达到16MS,这已经是非常快的速度了.
可以得到这样的结论:A*算法的运行速度与估价函数H()有关,估价函数越好,运行速度就越快.
3.2 四边形简单地图寻路算法
首先为什么叫四边形简单地图呢,因为这个实例选择了简单的二位数组当做地图,且通过各个点是没有地形附加因素的,即可以理解成简单的单位代价,在这样的情况下使用A*算法寻找最短路径.

我们根据上图对路径做出一定的规范:
- 采用了八连通的方法,但是不能穿过墙角.
- 相邻点代价取为10,斜线代价为
- 所以对于H函数的值最后也要*10
对于1的解释:比如在起点下方的斜线位置,必须先向下再向右,不能穿过墙角.
对于2的解释:10*sqrt(2)大致就是14(14.14…)
近似处理…
H()估价函数采用前面已学习的曼哈顿算法.
地图使用随机数生成.
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 |
#include <iostream> #include <queue> #include <cstdlib> using namespace std; struct node { int m_x; //节点的x坐标 int m_y; //节点的y坐标 int m_f; //F() int m_g; //G() bool operator <(const node &temp)const { return temp.m_f < m_f; } }; struct Point { int p_x; int p_y; }; const int Size_X = 16; //地图的横向大小 const int Size_Y = 16; //地图的纵向大小 const int Start_X = 0; //起点X坐标 const int Start_Y = 0; //起点Y坐标 const int End_X = Size_X-1; //终点X坐标 const int End_Y = Size_Y-1; //终点Y坐标 const int Rand = 70; //每100个大约70个空格 const int HB = 10; //H()的倍数 int dir[8][2] = { {-1, 0} //上 , { 0, 1} //右 , { 1, 0} //下 , { 0,-1} //左 , {-1, 1} //上右 , { 1, 1} //下右 , { 1,-1} //下左 , {-1,-1}}; //上左 int Map[Size_X][Size_Y]; //地图节点 int visit[Size_X][Size_Y]; //某个节点是否被访问过 0表示没访问过 Point pre[Size_X][Size_Y]; //记录当前节点的前一个节点的坐标值 //计算曼哈顿距离函数H() inline int H(int x,int y) { int result = 0; result += abs(x-End_X); result += abs(y-End_Y); return result*HB; } inline int Check(int x, int y) { if(x>=0 && x<Size_X && y>=0 && y<Size_Y ) { return 1; } else return 0; } inline int CheckCorner(int i ,int x ,int y) { if(i<4)return 1;//上下左右不判断墙角 int a = x+dir[i][0]; int b = y+dir[i][1]; if(!Map[a][y] || !Map[x][b]) { return 1; } return 0; } int bfs() { int x , y; priority_queue <node> q; node current , next; if(H(Start_X,Start_Y)==H(End_X,End_Y))return 1; current.m_g = 0; //当前节点的G()=0 current.m_f = H(Start_X,Start_Y); //当前节点的F()=0+H(); current.m_x = Start_X; current.m_y = Start_Y; visit[current.m_x][current.m_y] = 1; //首节点已访问。 q.push(current); //将首节点加入到队列中 while(!q.empty()) { current = q.top(); //获取第一个元素的值 q.pop(); //首元素出队 for(int i=0;i<8;i++) //八个方向依次遍历 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x += dir[i][0]; //然后对下一个节点的值进行修改 next.m_y += dir[i][1]; //如果下一个节点没有访问过 并且可以访问 if(!visit[next.m_x][next.m_y] && Check(next.m_x,next.m_y) && CheckCorner(i,current.m_x,current.m_y)) { //就访问下一个节点 if(i>=4) next.m_g += 14; //实际付出的代价+14 or 10 else next.m_g += 10; visit[next.m_x][next.m_y] = 1; //设置节点已访问 next.m_f = next.m_g + H(next.m_x,next.m_y); //F() = G() + H() pre[next.m_x][next.m_y].p_x = current.m_x; //前一个节点的X pre[next.m_x][next.m_y].p_y = current.m_y; //前一个节点的y if(H(next.m_x,next.m_y)==H(End_X,End_Y)) return 1; q.push(next); } } } return 0; } int main() { //随机生成地图 srand(unsigned(time(0))); for(int i=0;i<Size_X;i++) { for(int j=0;j<Size_Y;j++) { Map[i][j] = rand()%100; if(Map[i][j]>=Rand) { Map[i][j]=1;//墙 visit[i][j]=2; } else { Map[i][j]=0;//空地 visit[i][j]=0; } if((i==Start_X&&j==Start_Y)||(i==End_X)&&(j==End_Y)) { Map[i][j]=0; visit[i][j]=0; } cout << Map[i][j]<<" "; } cout << endl; } if(bfs()) { int x = End_X , y = End_Y; while(x!=Start_X || y!=Start_Y)//从终点开始搜索前一个结点,直到找到首节点 { Map[x][y] = 2;//设置路径 int temp_x=pre[x][y].p_x; int temp_y=pre[x][y].p_y; x = temp_x; y = temp_y; } system("cls"); for(int i=0;i<Size_X;i++) { for(int j=0;j<Size_Y;j++) { if(i==Start_X && j==Start_Y) cout << "S "; else if(i==End_X && j==End_Y) cout << "E "; else if(Map[i][j]==2) cout << "* "; else cout << Map[i][j]<<" "; } cout << endl; } } else { cout << "The Way Not Found"<<endl; } return 0; } |
但是,在某些情况下,结果会不太准确,比如:
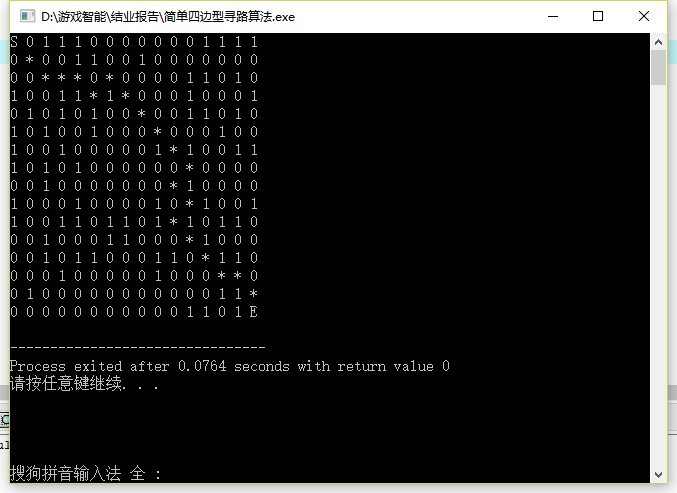
这种情况很明显的可以看出,在某些情况下,它宁愿选择开销更大的路径而不是开销更小的,只因为H()函数计算出的曼哈顿距离*10后的差值相比其他位置的4的差值更大一些.故可以适当调低倍数(HB),再进行测试。
3.3复杂地图寻路算法
这次的复杂地图是根据前面的简单地图做出的改进,
- 增加了地图的复杂性,通过不同的地形和长度所耗费的代价不一样
- 模拟真实的游戏地形,草地,澡泽,平原等…
需要解决的问题:
- H()函数相对以前需要更加的精细化.
- 因为地图的复杂性,所以H()函数需要更加的精细化.
- 如何模拟真实的游戏地形
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 |
#include <iostream> #include <queue> #include <cstdlib> using namespace std; struct node { int m_x; //节点的x坐标 int m_y; //节点的y坐标 int m_f; //F() int m_g; //G() bool operator <(const node &temp)const { return temp.m_f < m_f; } }; struct Point { int p_x; int p_y; }; const int Size_X = 16; //地图的横向大小 const int Size_Y = 16; //地图的纵向大小 const int Start_X = 0; //起点X坐标 const int Start_Y = 0; //起点Y坐标 const int End_X = Size_X-1; //终点X坐标 const int End_Y = Size_Y-1; //终点Y坐标 const int HB = 12; //H()的倍数 int dir[8][2] = { {-1, 0} //上 , { 0, 1} //右 , { 1, 0} //下 , { 0,-1} //左 , {-1, 1} //上右 , { 1, 1} //下右 , { 1,-1} //下左 , {-1,-1}}; //上左 int Map[Size_X][Size_Y]; //地图节点 int Count[Size_X][Size_Y]; //地图的权值 int visit[Size_X][Size_Y]; //某个节点是否被访问过 0表示没访问过 Point pre[Size_X][Size_Y]; //记录当前节点的前一个节点的坐标值 //计算曼哈顿距离函数H() inline int H(int x,int y) { int result = 0; result += abs(x-End_X); result += abs(y-End_Y); return result*HB; } inline int Check(int x, int y) { if(x>=0 && x<Size_X && y>=0 && y<Size_Y ) { return 1; } else return 0; } inline int CheckCorner(int i ,int x ,int y) { if(i<4)return 1;//上下左右不判断墙角 int a = x+dir[i][0]; int b = y+dir[i][1]; if(!Map[a][y] || !Map[x][b]) { return 1; } return 0; } int bfs() { int x , y; priority_queue <node> q; node current , next; if(H(Start_X,Start_Y)==H(End_X,End_Y))return 1; current.m_g = 0; //当前节点的G()=0 current.m_f = H(Start_X,Start_Y); //当前节点的F()=0+H(); current.m_x = Start_X; current.m_y = Start_Y; visit[current.m_x][current.m_y] = 1; //首节点已访问。 q.push(current); //将首节点加入到队列中 while(!q.empty()) { current = q.top(); //获取第一个元素的值 q.pop(); //首元素出队 for(int i=0;i<8;i++) //八个方向依次遍历 { next = current; //首先将当前节点的值赋给下一个节点 next.m_x += dir[i][0]; //然后对下一个节点的值进行修改 next.m_y += dir[i][1]; //如果下一个节点没有访问过 并且可以访问 if(!visit[next.m_x][next.m_y] && Check(next.m_x,next.m_y) && CheckCorner(i,current.m_x,current.m_y)) { //就访问下一个节点 if(i>=4) next.m_g += 1.4*Count[next.m_x][next.m_y]; else next.m_g += Count[next.m_x][next.m_y]; //实际付出的代价 visit[next.m_x][next.m_y] = 1; //设置节点已访问 next.m_f = next.m_g + H(next.m_x,next.m_y); //F() = G() + H() pre[next.m_x][next.m_y].p_x = current.m_x; //前一个节点的X pre[next.m_x][next.m_y].p_y = current.m_y; //前一个节点的y if(H(next.m_x,next.m_y)==H(End_X,End_Y)) return 1; q.push(next); } } } return 0; } int main() { //随机生成地图 srand(unsigned(time(0))); for(int i=0;i<Size_X;i++) { for(int j=0;j<Size_Y;j++) { Map[i][j] = rand()%100; if(Map[i][j]>=80) { Map[i][j]=9;//墙 Count[i][j]=32768; visit[i][j]=2; } else if(Map[i][j]>=60) { Map[i][j]=2;//澡泽 Count[i][j]=17; visit[i][j]=0; } else if(Map[i][j]>=40) { Map[i][j]=1;//草地 Count[i][j]=12; visit[i][j]=0; } else{ Map[i][j]=0;//平地 Count[i][j]=10; visit[i][j]=0; } if((i==Start_X&&j==Start_Y)||(i==End_X)&&(j==End_Y)) { Map[i][j]=0; Count[i][j]=0; visit[i][j]=0; } cout << Map[i][j]<<" "; } cout << endl; } if(bfs()) { int x = End_X , y = End_Y; while(x!=Start_X || y!=Start_Y)//从终点开始搜索前一个结点,直到找到首节点 { Map[x][y] = 5;//设置路径 int temp_x=pre[x][y].p_x; int temp_y=pre[x][y].p_y; x = temp_x; y = temp_y; } cout << endl; // system("cls"); for(int i=0;i<Size_X;i++) { for(int j=0;j<Size_Y;j++) { if(i==Start_X && j==Start_Y) cout << "S "; else if(i==End_X && j==End_Y) cout << "E "; else if(Map[i][j]==5) cout << "* "; else cout << Map[i][j]<<" "; } cout << endl; } } else { cout << "The Way Not Found"<<endl; } return 0; } |
注:以上代码还有部分需要修改的地方,不过实在是没时间了…
预计后期修改为:
- 修改地图的节点只允许一次访问,多次计算保证是最小的开销。
- 实在应该找一个漂亮点的界面
- 修改地图为六边形而不是四边形…
- 优化H()函数,得到最优值
- 使用小顶堆维护Open表而不是优先队列(这样会更快)
- 欢迎访问http://blog.tk-xiong.com/archives/232
参考文献
[1] 状态空间搜索——百度百科
[2] 启发式搜索算法——百度百科
[3] A*算法——百度百科
[4] 三种重要的启发式策略——新浪博客
[5] 人工智能——状态空间的搜索策略
[7] 八数码的八境界
[8] 康托展开和逆康展开——TK-Xiong’s Blog
[9] 曼哈顿距离——百度百科
来自TK Xiong

真牛X….,简直膜拜