双向链表…
相对于前一篇的Vector,List就稍微复杂了一些。
它的好处是每次插入或删除一个元素,就配置或者释放一个空间。
List对空间的运用十分精准,不会有一丝一毫的浪费。
对于已知位置的元素的插入与删除,List永远是常数时间O(1)
List的结点:
List的结点的结构如下:很明显这是一个双向链表…
|
1 2 3 4 5 6 7 8 |
template <class T> struct __list_node { typedef void* void_pointer; void_pointer prev; void_pointer next; T data; }; |
List的迭代器:
List的迭代器与Vector还是不一样的,因为List结点在空间中并不是连续存放的,所以必须重新设计一个迭代器。
需要完成的功能是:正确的 递增(指向下一个节点)、递减(指向上一个节点)、取值(取节点数据值)、成员存取(取节点的成员)等操作。
同时因为List的设计是一个双向链表,所以提供的是Bidirectional Iterators(双向迭代器)
List的一个重要性质是,插入操作(insert)和接合操作(splice)都不会造成原有的list的迭代器失效,删除操作(erase)也只有被删除的迭代器失效,对其他迭代器无影响。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
template<class T, class Ref, class Ptr> struct __list_iterator { typedef __list_iterator<T, T&, T*> iterator; typedef __list_iterator<T, Ref, Ptr> self; typedef bidirectional_iterator_tag iterator_category; //迭代器类型 typedef T value_type; //值类型 typedef Ptr pointer; //指针 typedef Ref reference; //引用 typedef __list_node<T>* link_type; //迭代器指向类型 typedef size_t size_type; //大小 typedef ptrdiff_t difference_type; //距离 link_type node; //指向一个结点 //construct//构造函数 __list_iterator(link_type x) : node(x) {} __list_iterator() {} __list_iterator(const iterator& x) : node(x.node) {} //运算符重载 bool operator==(const self& x) const { return node == x.node; } bool operator!=(const self& x) const { return node != x.node; } //对迭代器取值,取的是结点的数据值 reference operator* () const { return (*node).data; } //对迭代器成员存取 pointer operator-> () const { return &( operator*() ); } //前置加 self& operator++() { node = (link_type)((*node).next); return *this; } //后置加 self& operator++(int) { self tmp = *this; ++this; //调用前置加 return tmp; } //前置减 self& operator--() { node = (link_type)((*node).prev); return *this; } //后置减 self& operator--(int) { self tmp = *this; --this; //调用前置减 return tmp; } }; |
List的数据结构:
List不仅是一个双向链表,而且还是一个环状双向链表,它只需要一个指针,便可以完整表现整个链表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
template <class T, class Alloc = alloc> class list { protected: typedef __list_node<T> list_node; public: typedef list_node* link_type; protected: link_type node; //一个指针,表示整个环状双向链表 //...... }; |
如果让指针node指向刻意置于尾端的一个空白节点,node便能符合STL对于“前闭后开”区间的要求,成为last迭代器。
如图所示:
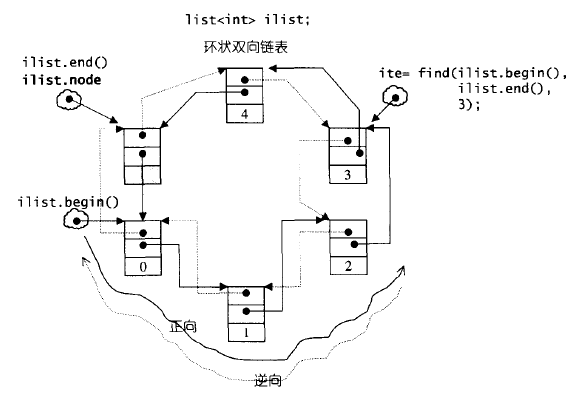
如此一来,以下几个函数便都可以轻易实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
iterator begin() { return (link_type)((*node).next); } iterator end() { return node; } bool empty() const { return node->next == node; } size_type size() const { size_type result = 0; distance(begin(), end(), result);//全局函数 return result; } reference front() { return *begin(); } reference back() { return *(--end()); } |
List的构造与内存管理:
construct, push_back, insert
4list-test.cpp :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
#include <list> #include <iostream> #include <algorithm> using namespace std; int main() { list <int>::iterator ite; //迭代器 list <int> ilist; //链表 //size = 0 cout << "size = " << ilist.size() << endl; ilist.push_back(0); ilist.push_back(1); ilist.push_back(2); ilist.push_back(3); ilist.push_back(4); //size = 5 cout << "size = " << ilist.size() << endl; //0 1 2 3 4 for(ite = ilist.begin() ; ite!=ilist.end() ; ite++) cout << *ite << " "; cout << endl; ite = find(ilist.begin(),ilist.end(),3); if(ite != ilist.end()) ilist.insert(ite,99); //size = 6 cout << "size = " << ilist.size() << endl; //3 cout << *ite << endl ; //0 1 2 99 3 4 for(ite = ilist.begin() ; ite!=ilist.end() ; ite++) cout << *ite << " "; cout << endl; //2 - 可以看出,删除前一个元素,返回指向后一个元素的迭代器 ite = find(ilist.begin(),ilist.end(),1); if(ite != ilist.end()) cout << *(ilist.erase(ite)) << endl; //0 2 99 3 4 for(ite = ilist.begin() ; ite!=ilist.end() ; ite++) cout << *ite << " "; cout << endl; return 0; } |
List缺省使用alloc作为空间配置器,并据此另外定义了一个list_node_allocator,为的是更方便地以节点大小为配置单位:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
protected: typedef simple_alloc<list_node, Alloc> list_node_allocator; protected: //配置一个结点并传回 link_type get_node() { return list_node_allocator::allocate(); } //释放一个结点 void put_node(link_type p) { list_node_allocator::deallocate(p); } //产生(配置并构造)一个结点,带元素值 link_type create_node(const T& x) { link_type p = get_node(); construct(&p->data, x); return p; } //销毁(析构并释放)一个结点 void destroy_node(link_type p) { destroy(&p->data); put_node(p); } public: //构造函数 list() { empty_initialize(); } protected: //初始化一个空链表 void empty_initialize() { node = get_node(); //配置一个结点空间,令node指向它 node->next = node; //头尾指针都指向自己,不设元素值 node->prev = node; } |
当我们调用 push_back时,此函数内部调用insert函数:
|
1 2 3 4 |
void push_back(const T& x) { insert(end(), x); } |
Insert函数是一个重载函数,有多种形式,最简单的一种如下:
配置并构造一个结点,然后在尾端进行指针操作,将节点插入。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
void push_back(const T& x) { insert(end(), x); } iterator insert(iterator position, const T& x) { //产生并配置一个结点 link_type tmp = create_node(x); //调整指针,将tmp插入到position前面 tmp->next = position.node; tmp->prev = position.node->prev; (link_type(position.node->prev))->next = tmp; position.node->prev = tmp; //返回插入的结点 return tmp; } |
List的元素操作:
push_front, push_back, erase, pop_front, pop_back, clear, remove, unique, merge, reverse, sort
List提供的元素操作很多,在此仅选侯捷大神书上写的记载。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
void push_back(const T& x) { insert(end(), x); } void push_front(const T& x) { insert(begin(), x); } iterator erase(iterator position) { link_type next_node = link_type(position.node->next); link_type prev_node = link_type(position.node->prev); //前一个节点的next指向后一个结点 prev_node->next = next_node; //后一个结点的prev指向前一个节点 next_node->prev = prev_node; //销毁(析构并释放)要删除的结点 destroy_node(position.node); //返回后一个结点 return iterator(next_node); } void pop_front() { erase(begin()); } void pop_back() { iterator tmp = end(); erase(--tmp); } |
以上这些是写在class内的,默认内联
然后还有一些稍复杂的定义在class外:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
//清除链表所有节点 template <class T, class Alloc> void list<T, Alloc>::clear() { link_type cur = (link_type) node->next; //遍历每一个结点并销毁释放 while(cur != node) { link_type tmp = cur; cur = (link_type)cur->next; destrot_node(tmp); } //恢复node为初始状态 node->next = node; node->prev = node; } //将数值为value之所有元素溢出 template <class T, class Alloc> void list<T, Alloc>::remove(const T& value) { iterator first = begin(); iterator last = end(); //遍历所有元素 while(first != last) { iterator next = first; ++ next; //如果值与value相等,则移除 if(*first == value) erase(first); first = next; } } //移除数值相同且连续的元素。 //注意!只有"连续且相同"的元素,才会被移除剩一个 template <class T, class Alloc> void list<T, Alloc>::unique() { iterator first = begin(); iterator last = end(); if(first == last)return ; //遍历所有元素 iterator next = first; while(++next != last) { //如果后一个与前一个相等,则移除后一个 if(*first == *next) erase(next); else first = next; next = first; } } |
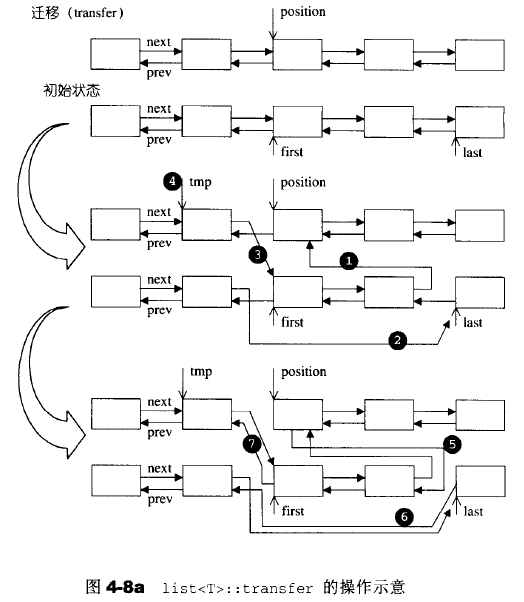
同时,List内部还提供一个迁移操作(transfer),它的作用是,将某连续范围内的元素迁移到某个特定位置之前。
技术上就是简单的结点指针移动,但是它为后面的 splice,sort,merge奠定良好的基础。
下面是transfer的源代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
protected: //将 [first,last) 之间的元素移动到 position 前面. void transfer(iterator position, iterator first, iterator last) { //如果相等,说明[first,last)就在position前面 if(position != last) { //1.last的前一个结点(要移动的最后一个元素)的next指针指向position. (*(link_type((*last.node).prev))).next = position.node; //2.first的前一个结点(第一个元素的前一个元素)的next指针指向last (*(link_type((*first.node).prev))).next = last.node; //3.position的前一个结点的next指向first (*(link_type((*position.node).prev))).next = first.node; //4.用一个tmp指向position的前一个结点(以备后用) link_type tmp = link_type((*position.node).prev); //5.position的prev指针指向last的前一个结点(要移动的最后一个元素) (*position.node).prev = (*last.node).prev; //6.last的prev指针指向first的前一个结点 (*last.node).prev = (*first.node).prev; //7.first的prev指针指向tmp (*first.node).prev = tmp; } } |
以下是示意图:
transfer并非公开的接口,list公开的接合操作实际上是splice。
可以在之前的 4list-test.cpp 程序最后再执行:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
int iv[5] = {5,6,7,8,9}; list <int> ilist2(iv, iv+5); //当前ilist为 0 2 99 3 4 ite = find(ilist.begin(), ilist.end(), 99); ilist.splice(itr, ilist2); //0 2 5 6 7 8 9 99 3 4 ilist.reverse(); //4 3 99 9 8 7 6 5 2 0 ilist.sort(); //0 2 3 4 5 6 7 8 9 99 |
为了适应不同的情况,splice有许多不的版本:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
public: //将x接合与position之前,x必须不同于this void splice(iterator position, list& x) { if(!x.empty()) { transfer(position, x.begin(), x.end()); } } //将 i 所指元素接合于position之前 void splice(iterator position, list& , iterator i) { iterator j = i; ++j; if(position == i || position == j) return ; transfer(position, i, j); } //将[first,last)区间内所有元素接合于 position 之前 // position不能位于[first,last)之内 void splice(iterator position, list& iterator first, iterator last) { if(first != last) { transfer(position, first, last); } } |
以下是merge(), reverse(), sort() 的源代码,有了transfer,这些操作都很简单。
Merge函数,要求两个list都已经提前排序好:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
template<class T, class Alloc> void list<T, Alloc>::merge(list<T, Alloc>& x) { iterator first1 = begin(); iterator last1 = end(); iterator first2 = x.begin(); iterator last2 = x.end(); //注意!前提是 两个list 都已经排序好的 while(first1 != last1 && first2 != last2) { if( *first2 < *first1) { iterator next = first2; transfer(first1, first2, ++next); first2 = next; } else ++first1; } if(first2 != last2) { transfer(last1, first2, last2); } } |
Reverse()函数,将*this的内容逆向重置:
做法是每次把未移动部分的首元素的后一个元素移动到begin()前面。
例如: (1 2 3) -> 2 (1 3) -> 3 2 (1) 完毕!
(1 2 3 4)->2 (1 3 4) -> 3 2 (1 4) -> 4 3 2 (1) 完毕!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
template<class T, class Alloc> void list<T, Alloc>::reverse() { //如果没有元素或者只有一个元素,则返回 if(node->next == node || link_type(node->next)->next == node) return ; iterator first = begin(); ++first; while(first != end()) { iterator old = first; ++ first; transfer(begin(), old, first); } } |
最后要注意的是,list不能使用STL自带的Sort算法,只能使用自己的sort()
因为STL的 sort算法只支持 RandomAccessIterator(随机存取迭代器)
本函数采用的是quicksort的方式。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
template<class T, class Alloc> void list<T, Alloc>::sort() { //如果为空或只有一个元素,就不进行任何操作 if(node->next==node || link_type(node->next)->next == node) return ; //创建一些新的lists,作为中介数据区 list<T, Alloc> carry; list<T, Alloc> counter[64]; int fill = 0; while(!empty()) { carry.splice(carry.begin(), *this, begin()); int i = 0; while(i < fill && !counter[i].empty()) { counter[i].merge(carry); carry.swap(counter[i++]); } carry.swap(counter[i]); if(i == fill) ++fill; } for(int i = 1; i < fill ; ++i) { counter[i].merge(counter[i-1]); } swap(counter[fill-1]); } |
说实话,这个排序我也还没看懂…我们慢慢来好吗?
…2016.7.17记于此。
7.18 后记:今天中午抽空模拟了一遍整个排序流程…
结果发现被坑!根本不是quick sort好么…用的归并的思想。

计算了一半其实就可以看出来了…这是归并排序的思想。
给了64个counter,所以能够排序的数量是2^64-1个数字,是很大的了。
时间复杂度呢,是n*log(n),这个不解释,归并都是这么快。
空间复杂度呢,是64个list(counter)和一个list(carry) 和一个fill,一个i…开销是很小的。
