【Algorithm】动态规划 – 小解

从不懂DP 到一维DP 到记忆化搜索到二维DP 到滚动数组到双向DP…

好了 – 以上已经是我DP的极限了…PS.整篇代码都是C/C++ – Java学习者慎入

DP 就是传说中的动态规划…啥叫动态规划…就是你要一边动一边规划…嗯，因为问题太难，所以经常看到一些人走来走去念念叨叨…咳咳，跑题了。

一句话概况动态规划的思想：通过先求出小问题的解组合来得到大问题的解。

这里举一个例子，一般我讲动态规划的时候，入门的例子都是它：

例1：Fibonacci 数列… 1 1 2 3 5 8 11… 嗯后面你们都知道了。

这个题目为啥叫动态规划呢…因为它就是根据前面的小问题的解得到大问题的解。

这个问题的DP方程是：

d[i] = d[i-1] + d[i-2]

1	d[i] = d[i-1] + d[i-2]

很简单对不对…就这么简单，我们就解决了这个问题…

然后贴一下代码：嗯，我这里是从第一项开始的。

#include <iostream>
using namespace std;

int D(int n)
{
	if(n<=2)return 1;
	return D(n-1) + D(n-2);
}

int main()
{
	cout << D(1) << endl;
	cout << D(2) << endl;	
	cout << D(3) << endl;
	cout << D(4) << endl;
	cout << D(5) << endl;
}

#include <iostream>

using namespace std;

int D(int n)

{

if(n<=2)return 1;

return D(n-1) + D(n-2);

}

int main()

{

cout << D(1) << endl;

cout << D(2) << endl;

cout << D(3) << endl;

cout << D(4) << endl;

cout << D(5) << endl;

}

好了，如果你能完全理解上面的代码，你就已经学会动态规划…的初级阶段了。

接下来我们对上面的代码进行优化。

我们来想想。我们计算D(5)的时候，内部进行了哪些计算。

要知道D(5) 我们得知道 D(3) 和 D(4) 对吧，要知道D(4)我们要知道D(3) 和 D(2)对吧，要知道D(3)我们得知道D(2) 和 D(1)对吧,那到这里我们发现，除了 D(1) 和 D(2) 是可以直接获得值之外，D(3)我们计算了两次…

这是数据比较小的情况，如果我们要计算 D(1000)呢…那得有多少重复计算呀…

所以我们用一个数组把值存储起来。代码如下：假设我们要计算D(1000)

#include <iostream>
using namespace std;

int d[1010] = {0}; 

int D(int n)
{
	if(d[n]==0)
	{
		d[n] = D(n-1) + D(n-2);
	}
	return d[n];
}

int main()
{
	d[1] = d[2] = 1;
	cout << D(1000);
}

#include <iostream>

using namespace std;

int d[1010] = {0};

int D(int n)

{

if(d[n]==0)

{

d[n] = D(n-1) + D(n-2);

}

return d[n];

}

int main()

{

d[1] = d[2] = 1;

cout << D(1000);

}

我们来分析一下，这里我并没有对特殊数据比如负数和0进行处理…因为我们只是思想的讲解。

我们先把所有数据初始化为0，表示没有计算过。接下来我们对第一项和第二项初始化为 1。

然后计算D (1000) ，很明显D(1000) 是没有计算过的，所以它会去计算D(999) 和 D(998)…

我们知道计算D(999) 需要得到D(998) 和 D(997) 的值，那么这样写的好处在哪里呢。

就是我们在计算D(999)的时候，已经计算过D(998)了，这样我们在计算完D(999)需要再计算D(998)的值的时候，就可以直接从数组中获得值，而不需要再次计算了。这样我们的计算速度可以更快。

听不懂？没事。画图！

Dp-优化

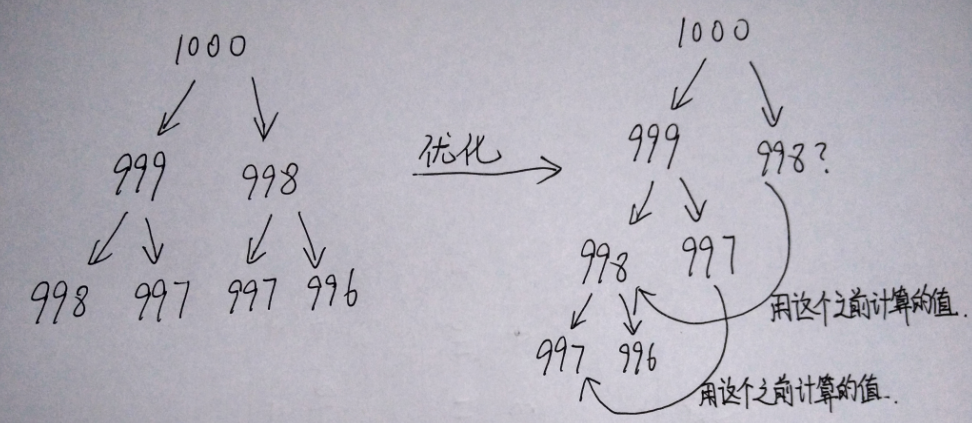
这样好理解了吧…我们的计算是沿着 1000->999->998->997->996这样递归下去的。然后当我们计算完了，返回到998的时候，因为 998在我们算999的时候已经算过了，就不需要再计算了。

现在我们来讲一个时间复杂度的概念…可以略去，建议看看。

如果我们不用优化的话，时间复杂度是 O(2^N)，如左图。

使用优化之后，我们的时间复杂度是O(N) ，如右图。因为我们需要的数据都只计算了一次。

这种优化方法就叫记忆化搜索，我们通过数组记住了前面计算的值。

PS. 还可以对空间进行优化…可以自己思考尝试一下。后面会讲到。

如果你还没有理解这个例子的话，我希望能够再多看几遍。手算一下。

如果你觉得你已经理解了这个问题。推荐题目如下：

爬楼梯：萌萌哒的MZ喜欢去红高粱吃饭，爬上红高粱一共有n步楼梯，他一次可以爬一步，也可以爬两步，问萌萌哒的MZ爬n层楼梯有多少种方式。
样例：
输入： 4
输出： 5

http://oj.tk-xiong.com/problem.php?id=1077

刚才我们讲到了一维的DP

现在我们来讲讲二维的DP：

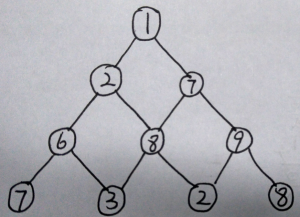DP-三角形题目描述：有一地图是这样的，我们只能往下走，假设每一格我们能获得若干个金币，问我们最多能获得多少个金币。
输入样例：
4
1
2 7
6 8 9
7 3 2 8
输出样例：
25
Hint: 1-> 7-> 9-> 8 这条路。

这道题的解决办法其实有两种：

穷举所有路径，获得最大值。
Dp动态规划。

因为我们是DP专题，这里就只讲解动态规划的方法。那么我们就得想办法把整条路这个大问题拆分成小问题。

我们通过分析题目，只能向下走。那么我们可以知道，中间的 8 这个数据，只可能从上面的 2 或者 7 走过来。

那么我们不考虑最后的最大值，我们考虑，我们到达某个点所能得到的最大利益。

比如我达到第二层第一个点(2) ，能获得的最大利益是 3

到达第二层第二个点的最大利益是 1+7 = 8

到达第三层第二个的最大利益是 Max(3+8,8+8) = 16;

最终我们能得到这一张图：

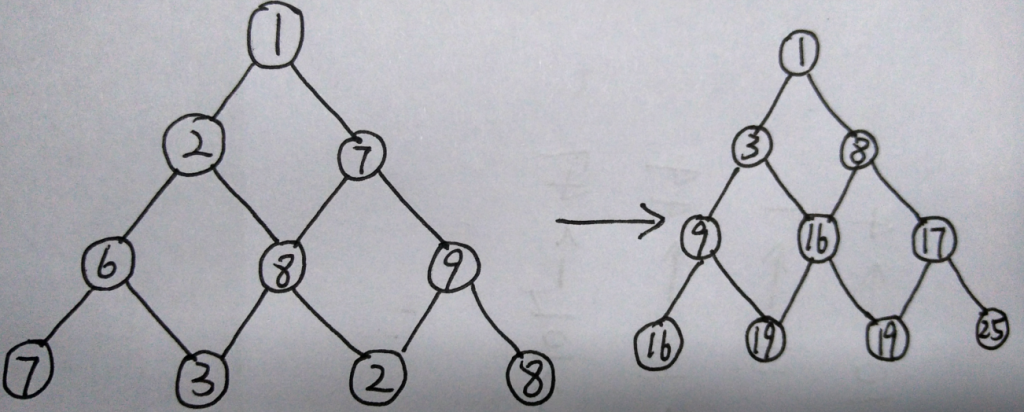
DP-优化三角形

右边的三角形的值是我们到达这个点能得到的金币数量…

最后我们的问题是：我们达到最下面的时候能够得到的最大金币数量。

那就遍历最下面一层的值，找到最大的25…完美！

这个题目和前一个题目是很像的…都是通过前一面的小问题的解得到当前问题的解。

题目链接：

http://oj.tk-xiong.com/problem.php?id=1078

接下来我们要讲的是 01背包问题。

这个是很经典的题目了。

题目描述：有n个物品，标号从1到n，第i个物品的价值为Vi，重量为Wi。现有一个袋子，最多能承受C重量的上限，求能装入物品的最大价值是多少？(物品不可拆分)

输入数据
先输入2个整数n，c，表示有n个物品和背包的装载量，然后接下来两行分别是输入物品的价值V 和重量W。

例如：

两个整数n,C：3 100

第一行价值V：30 25 20

第二行重量W：90 50 50

输出：

输出能够装载物品的最大价值。

例如：样例中最大价值是 25+20 = 45

故输出 45

输入样例：

3 100

30 25 20

90 50 50

输出样例：

当然这里我们不会用样例来进行演算，因为它太简单了…没有计算价值。

n = 5 ，C=10， V=[6,3,5,4,6]，W=[2,2,6,5,4]

问这种情况下我们得到的最大价值是多少。

我们可以把这个问题视为一个决策问题，即装与不装的问题…

如果我们把这个物品装入背包，那么这个决策我们视为1，如果不装，视为0.

所以这个问题是可以穷举所有情况来判断的。当然如果我们穷举这个问题，那也太傻了。

这个问题我们该怎么来做呢…视为一个决策问题，对第i个物品的决策是xi，每次操作产生的收益是增加价值xi*vi，因此总价值最大即是max ∑ xi.vi, i=1~n。约束条件是：如果物品i装入时超重，则只有不装入一种可选操作, 任何一个阶段i 的操作，需满足 ∑ xk.wk< C， k=1~i.

回忆动态规划的特征（最优子结构）：如果 x1,x2,…xn是n阶问题的最优解，则它的某个子段是小规模k阶问题的最优解。所以可先求解k<n问题，然后递推到第n步。

C,W,V作为常量，以2元组（n,c）表示考虑的问题， n是物品个数，c是背包容量。

如果(x1,x2,…xn）是问题（n,c）最优解，那么（ x1,x2,…xn -1）是什么？

1 当xn=0时，（ x1, x2, … xn -1）是 (n-1,c) 的最优解

2 当xn=1时，（ x1, x2, … xn -1）是 (n-1,c-wn) 的最优解

上述关系说明，如果将小规模问题1（n-1,c）和问题2 (n-1,c-wn) 求解了，那么（n,c）就可以得到。

以D[n][c] 记录问题（n,c）的最优价值，则：D[n][c]= max( D[n-1][c], D[n-1][c-wn]+vn)

如果用i,j做下标则是：D[i][j] = max( D[i-1][j], D[i-1][j-wi] + vi )

我们找到DP方程了！就是它 ↑ …

接下来就是递推关系演算：

来，让我们打表吧，上面的东西看不懂没关系。看懂这个公式和怎么填表就行了。

D[i][j] = max( D[i – 1][j], D[i – 1][j – wi] + vi )

根据物品和背包重量的关系：

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1
2
3
4
5

首先看上表…在物品数量为0的情况下和背包承重为0的情况下，肯定都是0…这个不解释哦

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	0	6	6	6	6	6	6	6	6	6
2
3
4
5

接下来是一个物品的情况… 这个物品重量是 2 价值是6…所以这种情况下都是6…

接下来是两个物品的情况，要关注的点是(2,2) – 即n=2 C=2，这种情况下是有比较的。

第二个物品的信息是重量是 2 价值是3

max( D[i – 1][j], D[i – 1][j – wi] + vi )

max(6,0+3) = 6. 很明显这里我们选择了不装第二个物品，而装第一个物品

然后接下来要关注的是 (2,4) – 即 n=2 C=4 …这种情况下两个物品都可以装的

max(6,6+3) = 9 很明显都装进去了嘛…

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	0	6	6	6	6	6	6	6	6	6
2	0	6	6	9	9	9	9	9	9	9
3
4
5

接下来是第三个物品…看，我们是不是在做 01决策了…这就是一个决策问题。

不慌，继续看…看完这个再回去看看理论部分，是不是清晰了很多。

第三个物品的信息是重量是 6 价值是5

数据有改变的点是(3,8) 即n=3 C=8和 (3,10)即n=3 C=10 。这个自己分析一下为什么。

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	0	6	6	6	6	6	6	6	6	6
2	0	6	6	9	9	9	9	9	9	9
3	0	6	6	9	9	9	9	11	11	14
4
5

接下来我们直接显示出完整的表：

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	0	6	6	6	6	6	6	6	6	6
2	0	6	6	9	9	9	9	9	9	9
3	0	6	6	9	9	9	9	11	11	14
4	0	6	6	9	9	9	10	11	13	14
5	0	6	6	9	9	12	12	15	15	15

所以我我们可以得出在物品数量为5，背包容量为10 的情况下，最大值是 15…

代码如下：

#include<iostream>
using namespace std;

int W[100];
int V[100];
int d[100][100];
int C;

int main()
{
	int n;
	cin >> n;
	cin >> C;
	for(int i=0;i<n;i++)
		cin >> V[i];
	for(int i=0;i<n;i++)
		cin >> W[i];

	for(int i=0;i<n;i++)	
	for(int j=0;j<=C;j++)
		d[i][j] = 0;
	
	for(int i=1;i<=n;i++)
	for(int k=0;k<=C;k++)
	{
		if(k >= W[i-1])
		{
			d[i][k] = max(d[i-1][k], d[i-1][k-W[i-1]] + V[i-1]);
		}
	}
	/*
	for(int i=0;i<=n;i++)
	{
		for(int k=0;k<=C;k++)
		{
			cout << d[i][k] << " "; 	
		}
		cout << endl;
	}
	*/
	cout << d[n][C];
}

#include<iostream>

using namespace std;

int W[100];

int V[100];

int d[100][100];

int C;

int main()

{

int n;

cin >> n;

cin >> C;

for(int i=0;i<n;i++)

cin >> V[i];

for(int i=0;i<n;i++)

cin >> W[i];

for(int i=0;i<n;i++)

for(int j=0;j<=C;j++)

d[i][j] = 0;

for(int i=1;i<=n;i++)

for(int k=0;k<=C;k++)

{

if(k >= W[i-1])

{

d[i][k] = max(d[i-1][k], d[i-1][k-W[i-1]] + V[i-1]);

}

for(int i=0;i<=n;i++)

{

for(int k=0;k<=C;k++)

{

cout << d[i][k] << " ";

}

cout << endl;

}

cout << d[n][C];

}

这里我留下来一行测试代码，来看打表的结果…

嗯，可以发现我们恰好得出了一个最优解，对吗。

接下来是对滚动数组的讲解…

首先我们回头看看斐波拉切数列这个题目…

我们可以发现，有一些数据用过了就不需要了。比如我们计算D(1000)的时候。只需要前两个D(999)和D(998)…前面的 997 和 996 都不需要了。

这就是我前面提到的还可以继续做空间优化。

优化代码如下：

#include <iostream>
using namespace std;

int main()
{
	int d[3];

	int n;
	while(cin >> n)
	{
		if(n == 0)
		{
			cout << 0 << endl;
			continue;
		}
		
		d[0] = 0;
		d[1] = 1;
		d[2] = 1;
		for(int i = 1; i < n; i++)
		{
			d[2] = d[1] + d[0];
			
			d[0] = d[1];
			d[1] = d[2];
		}
	
		cout << d[2] << endl;
	}
}

#include <iostream>

using namespace std;

int main()

{

int d[3];

int n;

while(cin >> n)

{

if(n == 0)

{

cout << 0 << endl;

continue;

}

d[0] = 0;

d[1] = 1;

d[2] = 1;

for(int i = 1; i < n; i++)

{

d[2] = d[1] + d[0];

d[0] = d[1];

d[1] = d[2];

}

cout << d[2] << endl;

}

这里…我就不解释了…是不是又优化了空间。但是对于多次计算，就会慢一些了。

现在我们来讲二维的滚动数组的优化…天呐，真是坑。我感觉心好累。

还记得我们之前填的表吗？这个…

n\C	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	0	6	6	6	6	6	6	6	6	6
2	0	6	6	9	9	9	9	9	9	9
3	0	6	6	9	9	9	9	11	11	14
4	0	6	6	9	9	9	10	11	13	14
5	0	6	6	9	9	12	12	15	15	15

你们有没有发现，我们填编号3的那一行的时候，用不到编号为1的数据，填编号为2的那一行的时候，用不到编号为0的行的数据。那这样是不是意味着我们可以只用两行呢？还可以再优化！只用一行！！！

我们从 C = 10 (最后)开始往前填写…依次覆盖即可。这样就不会导致数据冲突了…

代码如下：自己思考为啥哦…思考不清的话，就自己手动只用一行填写试试

#include<iostream>
using namespace std;

int W[100];
int V[100];
int d[100];
int C;

int main()
{
	int n;
	cin >> n;
	cin >> C;
	for(int i=0;i<n;i++)
		cin >> V[i];
	for(int i=0;i<n;i++)
		cin >> W[i];

	for(int j=0;j<=C;j++)
		d[j] = 0;
	
	for(int i=0;i<n;i++)
	for(int k = C;k>0;k--)
	{
		if(k >= W[i])
		{
			d[k] = max(d[k], d[k-W[i]] + V[i]);
		}
	}
	
	cout << d[C];
}

#include<iostream>

using namespace std;

int W[100];

int V[100];

int d[100];

int C;

int main()

{

int n;

cin >> n;

cin >> C;

for(int i=0;i<n;i++)

cin >> V[i];

for(int i=0;i<n;i++)

cin >> W[i];

for(int j=0;j<=C;j++)

d[j] = 0;

for(int i=0;i<n;i++)

for(int k = C;k>0;k--)

{

if(k >= W[i])

{

d[k] = max(d[k], d[k-W[i]] + V[i]);

}

cout << d[C];

}

好了滚动数组到这里就结束了…

接下来是双向DP…这个题目挺有意思的…当初优化的我都快疯了。

传纸条（一）

时间限制： 2000 ms | 内存限制： 65535 K 难度： 5

描述：小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个m行n列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用0表示），可以用一个0-1000的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入

第一行输入N(0<N<100)表示待测数据组数。

每组测试数据输入的第一行有2个用空格隔开的整数m和n，表示班里有m行n列（2<=m,n<=50）。

接下来的m行是一个m*n的矩阵，矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度（不大于1000）。每行的n个整数之间用空格隔开。

输出

每组测试数据输出共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

样例输入

3 3

0 3 9

2 8 5

5 7 0

样例输出

34

题目是一个双向dp的题目…

思路很明确，就是找那么一条路…从左上到右下，再从右下到左上…走过的路不允许重复。因为两条路来回的话，的确是不好做…所以转化为找两条从左上到右下的路…然后一条作为来的，一条作为回去的(是哪条无所谓)。

接下来就是找DP方程了…

首先我们定义 x1,y1 和 x2,y2 分别表示两条路上选择的点…

有题中规定，只能向下或向右走，则可得DP方程：

f(x1,y1,x2,y2) = max { f(x1-1, y1, x2-1, y2), f(x1-1, y1, x2, y-1), f(x1, y1-1, x2-1, y2), f(x1, y1-1, x2, y2-1)} + map[x1][y1] + map[x2][y2];

1	f(x1,y1,x2,y2) = max { f(x1-1, y1, x2-1, y2), f(x1-1, y1, x2, y-1), f(x1, y1-1, x2-1, y2), f(x1, y1-1, x2, y2-1)} + map[x1][y1] + map[x2][y2];

很长吧…事实就是这样…因为情况比较多嘛。

这样写的话时间复杂度会是O(n^4)，比较大…太慢了…会超时！对DP还是太慢了！

我们知道，每一次必定会向下或者向右走一步的。

因此有 x1+y1 == x2+y2 == k(新定义)

f(k,x1,x2) = max{ f(k-1, x1, x2), f(k-1, x-1, x2), f(k-1, x1, x2-1), f(k-1, x1-1, x2-1)} + map[x1][k-x1] + map[x2][k-x2];

1	f(k,x1,x2) = max{ f(k-1, x1, x2), f(k-1, x-1, x2), f(k-1, x1, x2-1), f(k-1, x1-1, x2-1)} + map[x1][k-x1] + map[x2][k-x2];

最后…根据滚动数组原理，优化代码如下：

/*
Author : xiong

用k替换x和y 表达成为 x1 = k ; y1 = k-x1 + 1;
循环关系为: 
从二维转化成一维要求从后往前覆盖 
d[y1] = Max(d[y1-1],d[y1]) + Map[x1][y1];

再转化为双线DP：
d[y1][y2]=Max(Max(d[y1-1][y2-1],d[y1-1][y2]),
			  Max(d[y1][y2-1],d[y1][y2]))
			 +Map[x1][y1]+Map[x2][y2];
即从二维->一维 然后推算成两个一维。
但是覆盖顺序不能乱了，不然会导致数据冲突。 
*/

#include <stdio.h>
#include <string.h>
#include <math.h>

#include <iostream>
#include <iomanip>		
#include <cstdlib>
#include <cstdio>
#include <string>
#include <cmath>

#include <algorithm>
#include <cassert>
#include <climits>
#include <ctime>
#include <vector> 
#include <queue>
#include <list>
#include <stack>
#include <map>

#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
 
using namespace std;

typedef long long LL;
typedef unsigned int Uint;
typedef unsigned long long ULL;
typedef long double LD;

int Map[52][52];
long d[52][52]; //这里数据得用long Uint存不下 

int main()
{
	DRI(N); 
	while(N--)
	{
	DRII(m,n);
	
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
		RI(Map[i][j]);
	
	for(int i=0;i<=51;i++)
	for(int j=0;j<=51;j++)
	d[i][j]=0;
	
	for(int k=2;k<m+n;k++)
		for(int x1=1;x1<=m;x1++)
		{
			int y1=k-x1+1;
			for(int x2=1;x2<=m;x2++)
			{
				int y2=k-x2+1;
				if(x1 != x2 && x1>0 && x2>0 && y1>0 && y2>0 && y1< n+1 && y2< n+1)
				{
					d[y1][y2] = max(
						max(d[y1-1][y2-1],d[y1-1][y2]),
						max(d[y1][y2-1],d[y1][y2]))
					+ Map[x1][y1] + Map[x2][y2];
				}
			}
		}
	
	Uint ans = max(d[n-1][n],d[n][n-1]);
	printf("%ld\n",ans);
	}
	return 0;
}

Author : xiong

用k替换x和y 表达成为 x1 = k ; y1 = k-x1 + 1;

循环关系为:

从二维转化成一维要求从后往前覆盖

d[y1] = Max(d[y1-1],d[y1]) + Map[x1][y1];

再转化为双线DP：

d[y1][y2]=Max(Max(d[y1-1][y2-1],d[y1-1][y2]),

Max(d[y1][y2-1],d[y1][y2]))

+Map[x1][y1]+Map[x2][y2];

即从二维->一维然后推算成两个一维。

但是覆盖顺序不能乱了，不然会导致数据冲突。

#include <stdio.h>

#include <string.h>

#include <math.h>

#include <iostream>

#include <iomanip>

#include <cstdlib>

#include <cstdio>

#include <string>

#include <cmath>

#include <algorithm>

#include <cassert>

#include <climits>

#include <ctime>

#include <vector>

#include <queue>

#include <list>

#include <stack>

#include <map>

#define RI(X) scanf("%d", &(X))

#define RII(X, Y) scanf("%d%d", &(X), &(Y))

#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))

#define DRI(X) int (X); scanf("%d", &X)

#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)

#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)

using namespace std;

typedef long long LL;

typedef unsigned int Uint;

typedef unsigned long long ULL;

typedef long double LD;

int Map[52][52];

long d[52][52]; //这里数据得用long Uint存不下

int main()

{

DRI(N);

while(N--)

{

DRII(m,n);

for(int i=1;i<=m;i++)

for(int j=1;j<=n;j++)

RI(Map[i][j]);

for(int i=0;i<=51;i++)

for(int j=0;j<=51;j++)

d[i][j]=0;

for(int k=2;k<m+n;k++)

for(int x1=1;x1<=m;x1++)

{

int y1=k-x1+1;

for(int x2=1;x2<=m;x2++)

{

int y2=k-x2+1;

if(x1 != x2 && x1>0 && x2>0 && y1>0 && y2>0 && y1< n+1 && y2< n+1)

{

d[y1][y2] = max(

max(d[y1-1][y2-1],d[y1-1][y2]),

max(d[y1][y2-1],d[y1][y2]))

+ Map[x1][y1] + Map[x2][y2];

}

Uint ans = max(d[n-1][n],d[n][n-1]);

printf("%ld\n",ans);

}

return 0;

}

或许不好理解…简单来讲就是根据前面的 滚动数组原理…把K这个本应该存储的值优化掉了…！

这样是优化到了最节省内存的情况了…

是不是跟疯了一样…当初做这个优化，我做了整整一个星期，但是至今骄傲。

恩恩，老大四狗滚回来又优化了一波：

速度：24 内存 240… 额时间第二，内存第四…

 #include <stdio.h>
#include <string.h>

int Max(const int &a, const int &b)
{
	if(a > b)
		return a;
	else 
		return b; 
}

int Min(const int &a, const int &b)
{
	if(a < b)
		return a;
	else 
		return b; 	
}

int main()
{
	int N;
	int m,n;
	int begin, end;	
	unsigned short Map[52][52] = {0};
	int d[52][52] = {0};
			
	scanf("%d",&N);
	while(N--)
	{
		scanf("%d %d",&m,&n);
				
		for(int i = 1; i <= m; i++)
		{
			for(int j = 1; j <= n; j++)
			{
				scanf("%d", &Map[i][j]);
			}
		}
	
		memset(d, 0, 10816);
			
		for(int k = 3; k < m+n; k++)
		{
			end = Min(m, k-1);
			begin = Max(k-n, 1);
			for(int x1 = end-1; x1 >= begin; --x1)
			{
				for(int x2 = end; x2 > x1; --x2)
				{
					d[x1][x2] = 
						Max( 
							Max(d[x1-1][x2-1], d[x1-1][x2]),
							Max(d[x1][x2-1], d[x1][x2])
						)
						+ Map[x1][k-x1]+Map[x2][k-x2];
				}
			}
		}
		
		printf("%d\n", Max(d[m-1][m], d[m][m-1]));
	}
	return 0;
}

#include <stdio.h>

#include <string.h>

int Max(const int &a, const int &b)

{

if(a > b)

return a;

else

return b;

}

int Min(const int &a, const int &b)

{

if(a < b)

return a;

else

return b;

}

int main()

{

int N;

int m,n;

int begin, end;

unsigned short Map[52][52] = {0};

int d[52][52] = {0};

scanf("%d",&N);

while(N--)

{

scanf("%d %d",&m,&n);

for(int i = 1; i <= m; i++)

{

for(int j = 1; j <= n; j++)

{

scanf("%d", &Map[i][j]);

}

memset(d, 0, 10816);

for(int k = 3; k < m+n; k++)

{

end = Min(m, k-1);

begin = Max(k-n, 1);

for(int x1 = end-1; x1 >= begin; --x1)

{

for(int x2 = end; x2 > x1; --x2)

{

d[x1][x2] =

Max(

Max(d[x1-1][x2-1], d[x1-1][x2]),

Max(d[x1][x2-1], d[x1][x2])

)

+ Map[x1][k-x1]+Map[x2][k-x2];

}

printf("%d\n", Max(d[m-1][m], d[m][m-1]));

}

return 0;

}

DP不是这么简单…这仅仅是入门罢了…到这里大致就结束了…但是应网友要求，再给出其他几个题目的解析和思路…

拓展题1：最长上升子序列.

其实这个问题比较经典的就是导弹拦截了。

前面有给出一个链接…http://oj.tk-xiong.com/problem.php?cid=1004&pid=4

题目思路：还是DP…

看看样例哈：

8
389 207 155 300 299 170 158 65

1 2	8 389 207 155 300 299 170 158 65

这个题目我们计算的是，对于每一个导弹在其前面的导弹高度符合要求的情况下的最大打下导弹数量加上这个导弹本身
对于第一个导弹可以直接打下为 1一个
对于第二个导弹由于是不能高于等于所以是满足要求的 2个了~
对于第三个导弹同样的继续打下 3个~
第四个导弹的时候，问题来了，因为它是大于155的…所以不能继续打了…这时候，我们要开始决策了…我们是放弃前面打掉的部分导弹，打掉它呢…还是怎么办。

老规矩打表…这个表的意思是，每一个导弹在其前面的导弹高度符合要求的情况下的最大打下导弹数量加上这个导弹本身。(只算前面的，不算后面的)

导弹高度	389	207	155	300	299	170	158	65
打下数量	1	2	3	2	3	4	5	6

打完表之后…我们要遍历一次这个表。找到最大值。

参考代码如下：

/*
Author : xiong

*/
#include <stdio.h>
#include <string.h>
#include <math.h>

#include <iostream>
#include <iomanip>		
#include <cstdlib>
#include <cstdio>
#include <string>
#include <cmath>

#include <algorithm>
#include <cassert>
#include <climits>
#include <ctime>
#include <vector> 
#include <queue>
#include <list>
#include <stack>
#include <map>

#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
 
using namespace std;

typedef long long LL;
typedef unsigned int Uint;
typedef unsigned long long ULL;
typedef long double LD;

int main()
{
	int H[20];
	int d[20];
	DRI(N);
	while(N--)
	{
		DRI(n);
		for(int i=0;i<n;i++)
		{
		RI(H[i]);
		d[i]=0;
		}

		int max=0;
		for(int i=0; i<n; i++)
		{
			//找到前面的合适的最大值
			for(int j=0; j<i; j++)
			{
				if(d[j]>d[i] && H[i]<H[j])
					d[i]=d[j];
			}
			d[i] += 1;
			if(d[i] > max) max = d[i];
		}
		
		printf("%d\n",max);
	}
}

Author : xiong

#include <stdio.h>

#include <string.h>

#include <math.h>

#include <iostream>

#include <iomanip>

#include <cstdlib>

#include <cstdio>

#include <string>

#include <cmath>

#include <algorithm>

#include <cassert>

#include <climits>

#include <ctime>

#include <vector>

#include <queue>

#include <list>

#include <stack>

#include <map>

#define RI(X) scanf("%d", &(X))

#define RII(X, Y) scanf("%d%d", &(X), &(Y))

#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))

#define DRI(X) int (X); scanf("%d", &X)

#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)

#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)

using namespace std;

typedef long long LL;

typedef unsigned int Uint;

typedef unsigned long long ULL;

typedef long double LD;

int main()

{

int H[20];

int d[20];

DRI(N);

while(N--)

{

DRI(n);

for(int i=0;i<n;i++)

{

RI(H[i]);

d[i]=0;

}

int max=0;

for(int i=0; i<n; i++)

{

//找到前面的合适的最大值

for(int j=0; j<i; j++)

{

if(d[j]>d[i] && H[i]<H[j])

d[i]=d[j];

}

d[i] += 1;

if(d[i] > max) max = d[i];

}

printf("%d\n",max);

}

这里还有一个NYOJ的题目放一下，现在OJ是可以访问的，我有空了也会把这道题放到我的OJ里，保证大家随时可以做题访问…

单调递增最长子序列：http://acm.nyist.net/JudgeOnline/problem.php?pid=17

同样给大家一段代码，这道题很简单。运行时间：2014-12-08 13:48:11 – 也是我大二的时候写的（我是先更新的下面的然后更新的上面的这个…嘻嘻）这里我觉得当时的思路还可以，虽然比较挫，还是来丢人现眼一下了。

/*
Author : xiong

DP方程:
d[i]表示以d[i]为终点的字串的单调递增最长子序列 

for(j=0;j<i;j++)
if(A[j]<A[i])
d[i]=max(d[i],d[j]+1);
*/

#include<stdio.h>
#include<string.h>
char A[10010];
int d[10010];
int len;

int Max(int a,int b)
{
	if(a>b)return a;
	else return b;
}

int main()
{
	int n;
	scanf("%d",&n);
	getchar();
	while(n--)
	{
		gets(A);
		len=strlen(A);
		
		for(int i=0;i<len;i++)
		d[i]=1;
		
		int max=0;
		for(int i=0;i<len;i++)
		{
			for(int j=0;j<i;j++)
				if(A[j]<A[i])
				d[i]=Max(d[j]+1,d[i]);
			if(d[i]>max)max=d[i];
		}
		printf("%d\n",max);
	}	
}

Author : xiong

DP方程:

d[i]表示以d[i]为终点的字串的单调递增最长子序列

for(j=0;j<i;j++)

if(A[j]<A[i])

d[i]=max(d[i],d[j]+1);

#include<stdio.h>

#include<string.h>

char A[10010];

int d[10010];

int len;

int Max(int a,int b)

{

if(a>b)return a;

else return b;

}

int main()

{

int n;

scanf("%d",&n);

getchar();

while(n--)

{

gets(A);

len=strlen(A);

for(int i=0;i<len;i++)

d[i]=1;

int max=0;

for(int i=0;i<len;i++)

{

for(int j=0;j<i;j++)

if(A[j]<A[i])

d[i]=Max(d[j]+1,d[i]);

if(d[i]>max)max=d[i];

}

printf("%d\n",max);

}

拓展题2：最长公共子序列.

这类题目经常有两个混淆不清，一个是最长公共子串，一个是最长公共子序列。

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。

而最长公共子序列则并不要求连续。

这个概念必须认识清楚。

然后接下来我们找一个最长公共子序列的题目，并对这个题目进行分析与解决。

就用NYOJ的题目吧…挺好的.http://acm.nyist.net/JudgeOnline/problem.php?pid=36

最长公共子序列 – 时间限制：3000 ms | 内存限制：65535 KB – 难度：3

描述：咱们就不拐弯抹角了，如题，需要你做的就是写一个程序，得出最长公共子序列。
tip：最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。其定义是，一个序列 S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列。

输入：第一行给出一个整数N(0<N<100)表示待测数据组数，接下来每组数据两行，分别为待测的两组字符串。每个字符串长度不大于1000.
输出：每组测试数据输出一个整数，表示最长公共子序列长度。每组结果占一行。
样例输入

2
asdf
adfsd
123abc
abc123abc

asdf

adfsd

123abc

abc123abc

样例输出

3
6

题目解析：

这个题目是我很久之前写的了…运行时间：2014-12-09 20:07:04 ，好像是大二上学期的事了。

回头看了一下，当初的代码真是龊的不行，所幸我还留有思路…这里给大家分析一下代码和思路。

/*
Author : xiong

DP:
d[i][j]表示：串A和串B当A在i,B在j位时取得的最长公共子序列的长度

if(A[i]==A[j])d[i][j] = d[i-1][j-1] + 1;
else d[i][j] = Max(d[i-1][j], d[i][j-1]);

*/

#include<stdio.h>
#include<string.h>
#define Max_Num 1010
	
char A[Max_Num];
char B[Max_Num];
int d[Max_Num][Max_Num];
int N,a,b;
	
int Max(int a,int b)
{
	if(a>b)return a;
	else return b;
}
	
int main()
{
	scanf("%d",&N);
	getchar();
	while(N--)
	{
		gets(A);
		gets(B);
		a=strlen(A);
		b=strlen(B);
		
		for(int i=0;i<a;i++)
		for(int j=0;j<b;j++)
		{
			d[i][j]=0;
		}
		
		for(int i=1;i<=a;i++)//处理不存在情况 
		for(int j=1;j<=b;j++)
		{
			if(A[i-1]==B[j-1])
			{
				d[i][j] = d[i-1][j-1] + 1;
			}
			else
			{
				d[i][j] = Max(d[i-1][j], d[i][j-1]);
			}
		}
		printf("%d\n",d[a][b]);
	}
}

Author : xiong

DP:

d[i][j]表示：串A和串B当A在i,B在j位时取得的最长公共子序列的长度

if(A[i]==A[j])d[i][j] = d[i-1][j-1] + 1;

else d[i][j] = Max(d[i-1][j], d[i][j-1]);

#include<stdio.h>

#include<string.h>

#define Max_Num 1010

char A[Max_Num];

char B[Max_Num];

int d[Max_Num][Max_Num];

int N,a,b;

int Max(int a,int b)

{

if(a>b)return a;

else return b;

}

int main()

{

scanf("%d",&N);

getchar();

while(N--)

{

gets(A);

gets(B);

a=strlen(A);

b=strlen(B);

for(int i=0;i<a;i++)

for(int j=0;j<b;j++)

{

d[i][j]=0;

}

for(int i=1;i<=a;i++)//处理不存在情况

for(int j=1;j<=b;j++)

{

if(A[i-1]==B[j-1])

{

d[i][j] = d[i-1][j-1] + 1;

}

else

{

d[i][j] = Max(d[i-1][j], d[i][j-1]);

}

printf("%d\n",d[a][b]);

}

当时代码其实对齐是没有这么工整的，但是现在看的时候，一眼就看懂了，新放上来还是改了一下。但是这些注释什么的，我可是一字不动，当我刚刚看到的时候，我只看了我注释的一句话，瞬间就想理解了这个题目的解法。相信大家也能够很快的学习并解决这个问题。

拓展题3：最大子段和 .

这个是新加的，因为我发现我们徐义春老师给的新的算法课本里面有这道题，就给学弟学妹们做一下。
这道题NYOJ里面没有…没办法，我就只能把书里的东西写一下了：
题目描述：
给定长度为n的整数序列 A={A0,A1,A2,A3…An-1};它的一个连续子段为{Ai,Ai+1,Ai+2…Aj};现要求求所有子段中，和值最大的子段。
输入：
首先输入一个整数n，表示序列中元素的数量。
然后输出一个整数序列，共有n个元素。
输出：
输出子段的首尾[begin,end]和最大和count。如果所有的字段和都小于0，则输出 -1 -1 0

输入样例：
8
1 -1 2 -3 6 7 -9 8
输出样例
4 5 13
样例解释：
最大值是6 + 7 ，下标为[4,5]，和为13.

这个题我过段时间会加到我的OJ里面去，供大家AC…嘻嘻

题目分析：
这个题目的话，最慢的方法就是穷举，穷举出所有的情况，时间复杂度是O(n3)，这样的话就太慢了。
然后优化的办法是使用前缀和。可以优化到O(n2)，在我看来还是比较慢。
这里其实是可以用动态规划的办法。因为它规定了是连续的。
所以可以用 d[i] 表示以这个点为字段的尾可以获得的最大值，这样我们记录一下前面有几个值，就可以获得首尾号和最大值了。没AC，知道思路对不对，我们来试试。

/*
Author : xiong

DP:
d[i] 表示以i为序列尾部时能获得的最大值。

if(d[i-1] > 0)
	d[i] = d[i-1] + A[i];
else
	d[i] = A[i];

这里要注意的是，d[i-1] == 0 的时候，我们该怎么办。
这里我们的决定是从新开始，前面的就不要了。
同时，最开始的预处理 d[0] = A[0];
*/ 

#include <iostream>
using namespace std;

int A[101];
int d[101];
int len[101];

int main()
{
	int n;
	cin >> n;
	
	for(int i = 0; i < n; i++)
	{
		cin >> A[i]; 
	}
	
	d[0] = A[0];
	len[0] = 0;
	for(int i = 1; i < n; i++)
	{
		if(d[i-1] > 0)
		{
			d[i] = A[i] + d[i-1];
			len[i] = len[i-1] + 1; 
		}
		else
		{
			d[i] = A[i];
			len[i] = 0;
		}
	}
	
	int max = 0; 
	for(int i = 1; i < n; i++)
	{
		if(d[i] > d[max])
		{
			max = i;
		}
	}
	
	if(d[max] < 0)
	{
		cout << -1 << -1 << 0 << endl;
	}
	else
	{ 
		cout << max-len[max] << " " << max << " " << d[max] << endl;
	}
}

Author : xiong

DP:

d[i] 表示以i为序列尾部时能获得的最大值。

if(d[i-1] > 0)

d[i] = d[i-1] + A[i];

else

d[i] = A[i];

这里要注意的是，d[i-1] == 0 的时候，我们该怎么办。

这里我们的决定是从新开始，前面的就不要了。

同时，最开始的预处理 d[0] = A[0];

#include <iostream>

using namespace std;

int A[101];

int d[101];

int len[101];

int main()

{

int n;

cin >> n;

for(int i = 0; i < n; i++)

{

cin >> A[i];

}

d[0] = A[0];

len[0] = 0;

for(int i = 1; i < n; i++)

{

if(d[i-1] > 0)

{

d[i] = A[i] + d[i-1];

len[i] = len[i-1] + 1;

}

else

{

d[i] = A[i];

len[i] = 0;

}

int max = 0;

for(int i = 1; i < n; i++)

{

if(d[i] > d[max])

{

max = i;

}

if(d[max] < 0)

{

cout << -1 << -1 << 0 << endl;

}

else

{

cout << max-len[max] << " " << max << " " << d[max] << endl;

}

代码不保证AC，因为没有题目可以AC…但是我觉得思路是对的了。供大家借鉴，如果有更好的获得下标方法，可以联系我。

拓展题4：合并石子 – 矩阵连乘.

首先是合并石子问题：

来自NYOJ：http://acm.nyist.net/JudgeOnline/problem.php?pid=737

石子合并（一） – 时间限制：1000 ms | 内存限制：65535 KB – 难度：3
题目描述：有N堆石子排成一排，每堆石子有一定的数量。现要将N堆石子并成为一堆。合并的过程只能每次将相邻的两堆石子堆成一堆，每次合并花费的代价为这两堆石子的和，经过N-1次合并后成为一堆。求出总的代价最小值。

输入描述：有多组测试数据，输入到文件结束(EOF)。
每组测试数据第一行有一个整数n，表示有n堆石子。
接下来的一行有n（0< n <200）个数，分别表示这n堆石子的数目，用空格隔开

输出描述：输出总代价的最小值，占单独的一行

样例输入

3
1 2 3
7
13 7 8 16 21 4 18

1 2 3

13 7 8 16 21 4 18

样例输出

9
239

239

题目思路：本来想到哈夫曼的，忽然发现只能把相邻的合并起来，那不是乖乖DP…

这里就不做具体的优化了。直接上代码吧。

/*
Author : Xiong

解题思路：乖乖DP吧...
d[i][j] 表示将石子 A[i],A[i+1]...A[j]合并起来的最小值。
而且要注意，合并的时候，应该是从中间取一个k
然后将 A[i]..A[k]这堆之前合并好的 与 A[k+1]...A[j]这另一堆合并起来 

所以有如下dp公式 
d[i][j] = min( d[i][k] + d[k+1][j] + Sum(A[i]...A[j]) ), 1 <= i <= k < j <= n 

最后引入一个前缀和的概念，因为我们要 Sum(A[i]...A[j])
如果一直加的话会很慢。所以我们令 : Q[i] = Sum(A[0],A[i]); //A[0] = 0;
这样 Sum(A[i]...A[j]) = Q[j] - Q[i-1]; 

*/

#include <iostream>
#include <queue>
#include <algorithm>
#include <climits>
#include <cstring>
using namespace std;

const int N = 200 + 1;

int A[N];	//石子数量 
int d[N][N];//dp
int Q[N]; 	//前缀和 

int DP(int i, int j)
{
	if(d[i][j] != -1)
	{
		return d[i][j];
	}
	
	if(i == j)
	{
		d[i][j] = 0;
		return d[i][j];
	}

	int min = INT_MAX;
	int temp = 0;
	for(int k = i; k < j; k++)
	{
		temp = DP(i, k) + DP(k+1, j);
		if(min > temp)
		{
			min = temp;
		}
	}
	d[i][j] = min + Q[j] - Q[i-1];
	return d[i][j];
}

int main()
{
	int n;
	while(cin >> n)
	{
		A[0] = 0;
		Q[0] = 0;
		for(int i = 1; i <= n; i++)
		{
			cin >> A[i];
		} 
		for(int i = 1; i <= n; i++)
		{
			Q[i] = Q[i-1] + A[i];
		} 
		
		memset(d, -1, sizeof(int)*N*N);
		
		cout << DP(1,n) << endl;
	}
}

Author : Xiong

解题思路：乖乖DP吧...

d[i][j] 表示将石子 A[i],A[i+1]...A[j]合并起来的最小值。

而且要注意，合并的时候，应该是从中间取一个k

然后将 A[i]..A[k]这堆之前合并好的与 A[k+1]...A[j]这另一堆合并起来

所以有如下dp公式

d[i][j] = min( d[i][k] + d[k+1][j] + Sum(A[i]...A[j]) ), 1 <= i <= k < j <= n

最后引入一个前缀和的概念，因为我们要 Sum(A[i]...A[j])

如果一直加的话会很慢。所以我们令 : Q[i] = Sum(A[0],A[i]); //A[0] = 0;

这样 Sum(A[i]...A[j]) = Q[j] - Q[i-1];

#include <iostream>

#include <queue>

#include <algorithm>

#include <climits>

#include <cstring>

using namespace std;

const int N = 200 + 1;

int A[N]; //石子数量

int d[N][N];//dp

int Q[N]; //前缀和

int DP(int i, int j)

{

if(d[i][j] != -1)

{

return d[i][j];

}

if(i == j)

{

d[i][j] = 0;

return d[i][j];

}

int min = INT_MAX;

int temp = 0;

for(int k = i; k < j; k++)

{

temp = DP(i, k) + DP(k+1, j);

if(min > temp)

{

min = temp;

}

d[i][j] = min + Q[j] - Q[i-1];

return d[i][j];

}

int main()

{

int n;

while(cin >> n)

{

A[0] = 0;

Q[0] = 0;

for(int i = 1; i <= n; i++)

{

cin >> A[i];

}

for(int i = 1; i <= n; i++)

{

Q[i] = Q[i-1] + A[i];

}

memset(d, -1, sizeof(int)*N*N);

cout << DP(1,n) << endl;

}

确认AC，但是不快…懒得优化了。

然后接下来找一个矩阵连乘的题目，简单讲讲吧，一个意思的。

矩阵连乘问题 – 问题描述：

n个矩阵A1,A2,A3,…,An，如果其维度分别为d0*d1,d1*d2,d2*d3,…,dn-1*dn，则可以进行连乘运算M=A1·A2·A3·…·An。

根据矩阵乘法的定义，一个维度为a*b和一个维度为b*c的矩阵进行相乘运算时，需要做a*b*c次元素乘法运算。

多个矩阵的连乘满足结合律，不同结合顺序所需时间不一样。

以A1、A2、A3为例，可以有两种不同的顺序进行相乘，如果以(A1A2)A3的方式相乘，则总的元素乘法运算次数为d0·d1·d2 + d0·d2·d3，而如果采用A1(A2A3)这样的方式相乘的话，元素的乘法运算次数为d0·d1·d3 + d1·d2·d3。这两种情况下的计算次数可能是不一样的，例如如果d3>d2 && d1>d0，则后者需要的乘法次数会更多。

n个矩阵有更多的结合方式，每种方式带来不同的元素乘法次数。现要确定一种最佳的结合方式，使得元素乘法总次数最少，从而可以提高计算效率。

输入描述：

输入有两行，第一行有一个整数n，表示有n个矩阵。

接下来一行有n+1个数据，记录了矩阵的维度：d0,d1,d2,d3,…,dn

输出描述：

输出最少的乘法计算量和最佳的计算次序。

输入样例：

3
2 4 1 3

2 4 1 3

输出样例：

14
1 3 2
1 2 1

1 3 2

1 2 1

示例代码：

/*
Author : xiong

矩阵连乘问题 ：
	假设不仅要计算最小乘法计算量，还要得到最佳的计算次序。
	我们以d记录矩阵维度，第i个矩阵的维度为 d[i-1] 和 d[i] 
	以D[i][j]表示从i到j这么多个矩阵连乘的最小乘法计算量
	以B[i][j]表示从i到j这么多个矩阵的最佳策略是从哪个地方乘 

DP公式：
D[i][j] = min(D[i][k] + D[k+1][j] + d[i-1]*d[k]*d[j]);
其中 i <= k < j
然后在获得最小值的情况下：
B[i][j] = k;

*/ 

#include <iostream>
#include <climits>
#include <cstring>
using namespace std;

const int SIZE_N = 101;

int d[SIZE_N];
int D[SIZE_N][SIZE_N];
int B[SIZE_N][SIZE_N];

//DP计算，用来计算i-j矩阵连乘的最佳策略 
int DP(int i, int j)
{
	if(D[i][j] != -1)
	{
		return D[i][j];
	}
	
	if(i == j)
	{
		D[i][j] = 0;
		B[i][j] = i;
		return D[i][j];
	}
	
	D[i][j] = INT_MAX;
	int temp = 0;
	for(int k = i; k < j; k++)
	{
		temp = DP(i, k) + DP(k+1, j) + d[i-1]*d[k]*d[j];
		if(temp < D[i][j])
		{
			D[i][j] = temp;
			B[i][j] = k;
		}
	}
	return D[i][j];
}

//打印输出函数，输出i-j的最佳策略 
void MulOrder(int i, int j)
{
	cout << i << " " << j << " " << B[i][j] << endl;
	if(i < B[i][j])
	{
		MulOrder(i, B[i][j]);
	}
	if(B[i][j]+1 < j)
	{
		MulOrder(B[i][j]+1, j);
	}
}

int main()
{
	int n;
	cin >> n;
	for(int i = 0; i <= n; i++)
	{
		cin >> d[i];
	}
	
	memset(D,-1,sizeof(int)*SIZE_N*SIZE_N);
	
	cout << DP(1, n) << endl;
	
	MulOrder(1, n);
}

Author : xiong

矩阵连乘问题：

假设不仅要计算最小乘法计算量，还要得到最佳的计算次序。

我们以d记录矩阵维度，第i个矩阵的维度为 d[i-1] 和 d[i]

以D[i][j]表示从i到j这么多个矩阵连乘的最小乘法计算量

以B[i][j]表示从i到j这么多个矩阵的最佳策略是从哪个地方乘

DP公式：

D[i][j] = min(D[i][k] + D[k+1][j] + d[i-1]*d[k]*d[j]);

其中 i <= k < j

然后在获得最小值的情况下：

B[i][j] = k;

#include <iostream>

#include <climits>

#include <cstring>

using namespace std;

const int SIZE_N = 101;

int d[SIZE_N];

int D[SIZE_N][SIZE_N];

int B[SIZE_N][SIZE_N];

//DP计算，用来计算i-j矩阵连乘的最佳策略

int DP(int i, int j)

{

if(D[i][j] != -1)

{

return D[i][j];

}

if(i == j)

{

D[i][j] = 0;

B[i][j] = i;

return D[i][j];

}

D[i][j] = INT_MAX;

int temp = 0;

for(int k = i; k < j; k++)

{

temp = DP(i, k) + DP(k+1, j) + d[i-1]*d[k]*d[j];

if(temp < D[i][j])

{

D[i][j] = temp;

B[i][j] = k;

}

return D[i][j];

}

//打印输出函数，输出i-j的最佳策略

void MulOrder(int i, int j)

{

cout << i << " " << j << " " << B[i][j] << endl;

if(i < B[i][j])

{

MulOrder(i, B[i][j]);

}

if(B[i][j]+1 < j)

{

MulOrder(B[i][j]+1, j);

}

int main()

{

int n;

cin >> n;

for(int i = 0; i <= n; i++)

{

cin >> d[i];

}

memset(D,-1,sizeof(int)*SIZE_N*SIZE_N);

cout << DP(1, n) << endl;

MulOrder(1, n);

}

拓展题5：最优二叉树搜索.

拓展题6：字符串变换问题.

以上都是建议题目…近期较忙。会挂在这里。有时间会搜索出这篇文章进行更新的额。

Flag：未完待续…

【Algorithm】动态规划 – 小解

Tagged on: Algorithm C++ Code