这里只讲 QuickSort(快排)、HeapSort(堆排)、MergeSort(归并)、ShellSort(希尔)。
首先是各个排序算法的时间空间复杂度。(不是我做的…)
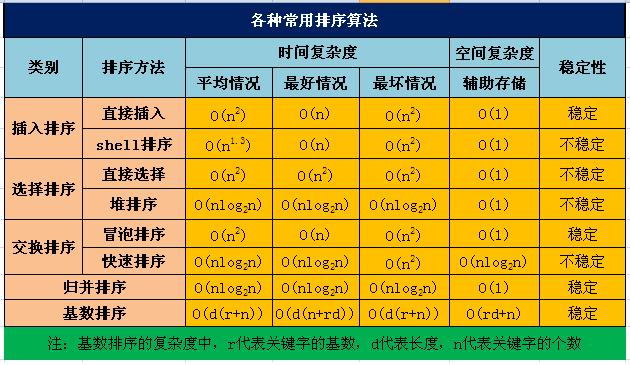
然后会讲Shell排序、堆排序、快速排序、归并排序。
先讲快速排序吧:
快速排序是找出一个元素(理论上可以随便找一个)作为基准(pivot),然后对数组进行分区操作,使基准左边元素的值都不大于基准值,基准右边的元素值 都不小于基准值,如此作为基准的元素调整到排序后的正确位置。
递归快速排序,将其他n-1个元素也调整到排序后的正确位置。
最后每个元素都是在排序后的正 确位置,排序完成。
所以快速排序算法的核心算法是分区操作,即如何调整基准的位置以及调整返回基准的最终位置以便分治递归。
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
#include <iostream> using namespace std; void QuickSort(int A[], int begin, int end) { if(begin < end) { int key = A[begin]; int left = begin; int right = end; while(left < right) { while(left < right && A[right] > key) { right --; } A[left] = A[right]; while(left < right && A[left] < key) { left ++; } A[right] = A[left]; } A[left] = key; QuickSort(A,begin,left-1); QuickSort(A,left+1,end); } } int main() { int A[5] = {5,2,1,3,4}; QuickSort(A,0,4); for(int i=0;i<5;i++) { cout << A[i] << " "; } cout << endl; } |
堆排序:
在我眼里就是三步,建堆,交换,调整。
建堆是从下到上调整为大根堆或者小根堆(即从最后一个非叶子节点开始),若用数组存储,则最后一个非叶子节点应该是size/2。例如:12345,他们的下标是01234,size=5,最后一个非叶子节点是2。
调整节点的过程如下:先判断左右子树大小,如果左子树小于或大于右子树,则用右子树的值和节点的值进行交换,然后再调整用来交换的子树,比如刚才交换的是左子树和节点,则调整左子树,否则调整右子树。
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#include<iostream> using namespace std; void HeapAdjust(int A[], int i, int size) { int lChild = 2*i; int rChild = 2*i+1; if(i <= size/2) { int max = lChild; if(lChild <= size && rChild <= size && A[lChild] < A[rChild]) { max = rChild; } if(max <= size && A[max] > A[i]) { swap(A[max],A[i]); HeapAdjust(A,max,size); } } } void HeapBuild(int A[], int size) { for(int i=size/2; i>=1; --i) { HeapAdjust(A,i,size); } } void HeapSort(int A[], int size) { HeapBuild(A,size); //建堆 for(int i=size; i>=2; --i) { swap(A[1],A[i]); //交换 HeapAdjust(A,1,i-1);//调整 } } int main() { int A[21] = {0,3,6,8,7,9,5,1,4,2,10,11,13,12,14,15,16,17,18,19,20}; HeapSort(A,20); for(int i=1;i<=20;i++) { cout << A[i] << " "; } cout << endl; } |
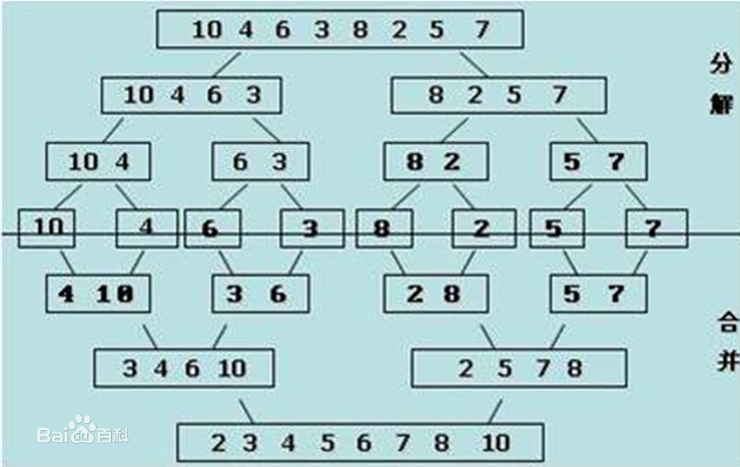
归并排序:
分治法,先排序左边,再排序右边,再合并。
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
#include <iostream> using namespace std; void Merge(int A[], int begin, int mid, int end) { int B[end-begin]; int i = begin; int j = mid; int k = 0; while(i<mid && j<end) { if(A[i]<A[j]) { B[k++] = A[i++]; } else { B[k++] = A[j++]; } } while(i<mid) { B[k++] = A[i++]; } while(j<end) { B[k++] = A[j++]; } for(int i=begin;i<end;i++) { A[i] = B[i-begin]; } } void MergeSort(int A[], int begin, int end) { if(begin < end-1)//元素为1个时停止 { int mid = (begin+end)/2; MergeSort(A,begin,mid); //左半边排序 MergeSort(A,mid,end); //右半边排序 Merge(A,begin,mid,end); //归并 } } int main() { int A[10] = {1,3,5,7,9,2,4,6,8,10}; MergeSort(A,0,10); for(int i=0;i<10;i++) { cout << A[i] << " "; } cout << endl; } |
最后是Shell排序,又叫缩小增量排序法…
算法思想:将待排序的序列分割成若干个子序列,分别进行插入排序。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <iostream> using namespace std; void ShellInsert(int A[],int size,int delta) { for(int i = delta; i<size; i++) { if(A[i] < A[i-delta]) { int key = A[i]; int j; for(j = i-delta;j>=0 && key < A[j]; j-=delta) { A[j+delta] = A[j]; } A[j+delta] = key; } } } void ShellSort(int A[], int size, int delta[] , int n) { for(int i=0;i<n;i++) { ShellInsert(A,size,delta[i]); } } int main() { int A[10] = {1,3,7,5,9,2,6,8,4,10}; int delta[10] = {5,2,1}; ShellSort(A,10,delta,3); for(int i=0; i<10; i++) { cout << A[i] << " "; } cout << endl; } |
大致就是这四个…效率比较高的…我一般喜欢归并,因为效率高,思路简单…
【Sort】排序算法小结.
