【Tree】平衡二叉排序树的四种旋转

LL、LR、RL、RR四种旋转方式解析。

LL：

假设最低层失衡节点为A，在结点A的左子树的左子树插入新结点S后导致失衡。如下图所示：

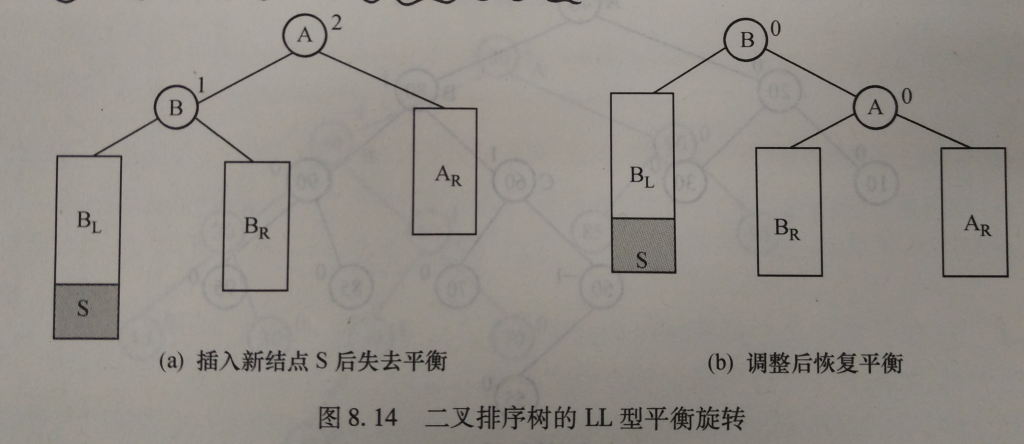
由A和B的平衡因子可以推知：BL BR 和 AR 深度相同，为恢复平衡，可采用如下方法：

1. 将A改为B的右孩子
2. B原来的右孩子改为A的左孩子

这相当于以B为轴，对A进行一次顺时针旋转。

代码如下：

然后：因为这时候B变成了根，所以要将A的父指针FA指向B，代码如下：

 

---

 

 

LR型：

假设最底层失衡节点为A，在结点A的左子树的右子树插入新节点S后导致失衡。如下图所示：

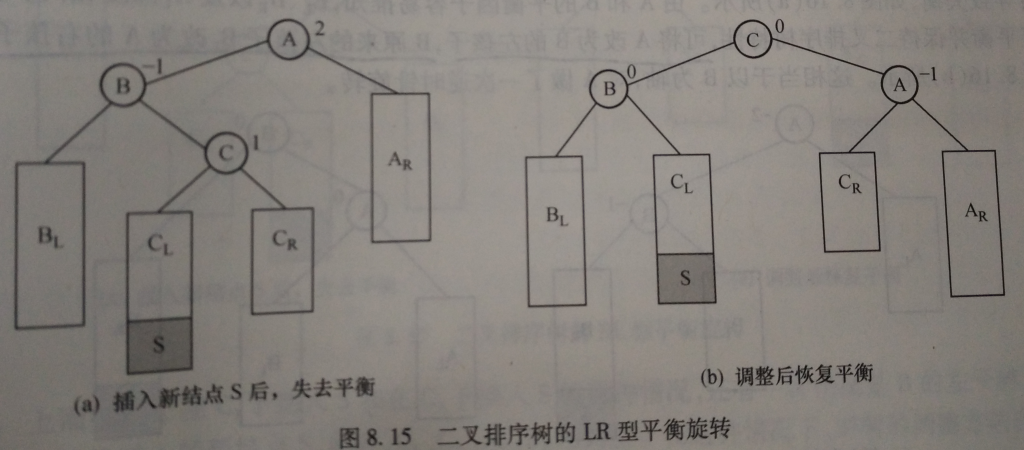
这里假设的是在CL下插入S，如果是在CR下插入S，调整方法相同，只是调整后A和B的平衡因子不同。

由ABC的平衡因子可以推知：CL与CR深度相同，BL与AR深度相同。且BL、AR的深度比CL、CR的深度大1.

为保持平衡二叉树的恢复特性，可以采用如下方法修改：

1. 将B改为C的左孩子
2. C的左孩子改为B的右孩子
3. A改为C的右孩子
4. C的右孩子改为A的左孩子。

认真看可以发现是对B的一次 RR 旋转， 然后是对A的 LL 旋转.

代码如下：

修改父节点的代码把前面的B换成C即可…

---

RR型：

RR型与LL型是对称的。

假设最底层失衡节点是A，在结点A的右子树的右子树插入新的结点S后导致失衡。如下图所示：

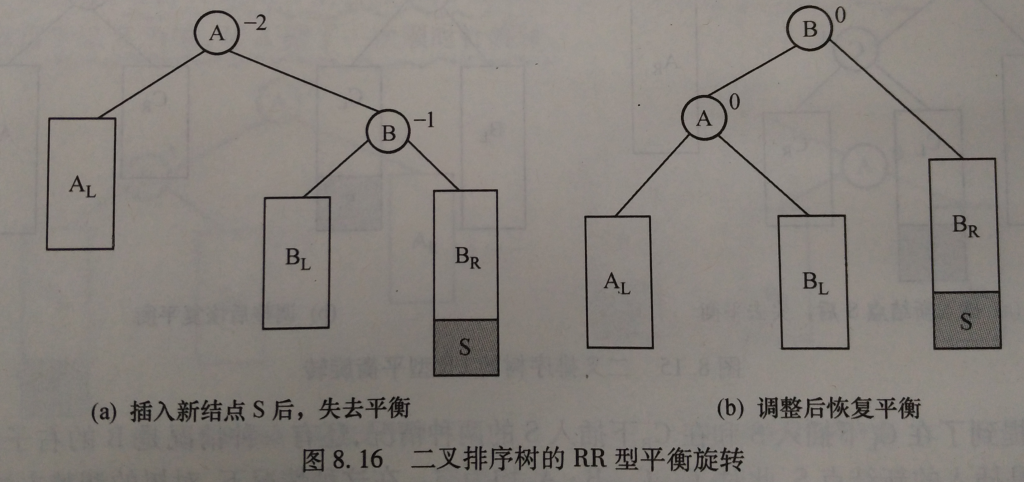
由A和B的平衡因子可知：原来的BL，BR以及AL的深度相同。

为恢复平衡保持二叉树的特性：修改方法如下：

1. A改为B的左孩子
2. B的左孩子改为A的右孩子

代码如下：

调整父节点代码与LL相同。

---

 

RL型：与LR型是对称的。

假设最低失衡结点是A，在结点A的右子树的左子树插入S后导致失衡。如下图所示：

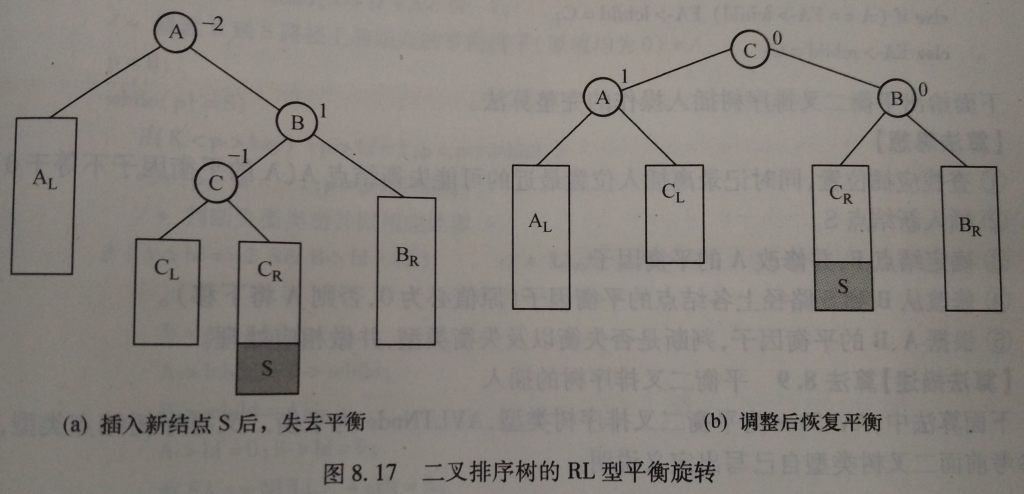
这里假设在CR下插入S，如果是在CL下插入S调整方法相同，只是调整后平衡因子不同。

由ABC的平衡因子可以推知：CL和CR深度相同，AL与BR深度相同，且AL、BR深度比CL、CR深度大1.

恢复方法：

1. B改为C右孩子
2. C原来右孩子CR改为B的左孩子
3. A改为C的左孩子
4. C原来左孩子CL改为A的右孩子

代码如下：

最后的父指针调整方法与LR相同。

大致就是这样吧。。。