红黑树-关联式容器的底层实现之一
在前面我们讲到了容器分为大致两种,一种序列式的,一种关联式的。
这里要讲的就是关联式容器的底层机制之一 红黑树
在讲红黑树之前,我们必须要明白 二叉搜素树,平衡二叉搜素树,旋转等概念。
所以可以先参考这几篇博客:
二叉搜索树:http://blog.tk-xiong.com/archives/476
平衡二叉搜索树:http://blog.tk-xiong.com/archives/492
四种旋转 http://blog.tk-xiong.com/archives/494
接下来的文章都默认以上内容读者是已经清楚明了的…
RB-Tree(红黑树)
除了AVL树之外,还有一种平衡二叉搜索树叫做RB-Tree
除了是一个二叉搜索树之外,还具有以下规则:
- 每个节点不是红色就是黑色
- 根结点为黑色
- 如果一个结点为红色,则它的子节点必须为黑色
- 任一节点到树尾端(NULL)的任何路径,黑色节点数量必须相同
遵守以上规则,我们才能得到一个标准的RB-Tree.
RB-Tree 插入节点:
根据前面提到的规则4,我们可以得到以下结论:新插入的结点必须是红色
然后根据规则3,我们可以知道新插入的结点的父节点必须是黑色
如果新插入的结点不满足上述条件时,就必须调整颜色,旋转树形。
首先我们来看看下图,分析一下为什么下面这几种情况都不合理:
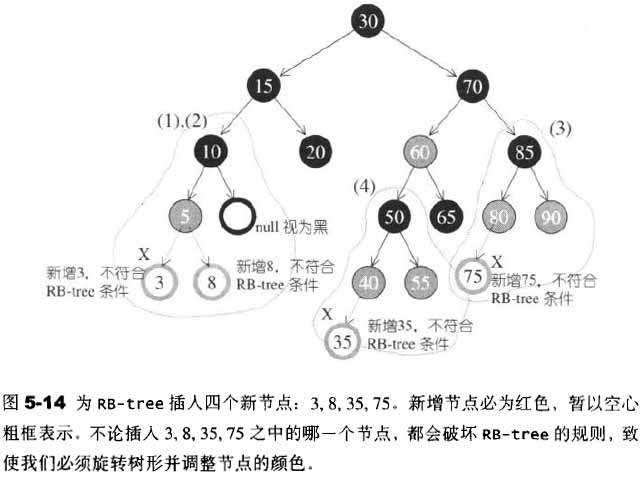
分析完上述的原因后,我们会根据以下四种情况进行旋转变色调整。
当然为了方便我们进行讨论,做出以下规定:
- 新插入节点为X
- 父节点为P
- 祖父节点为G
- 父节点的兄弟节点为S
- 曾祖父节点为G&G
根据RB-Tree的规则,我们知道,X的颜色必为红色。
如果P也是红色,则会违反规则,就需要调整
如果P是黑色,不会违反规则
那么根据规则3,我们可以知道P的父节点G肯定是黑色。(规则3)
于是我们可以得到同旋转一样的以下四种情况:
这里我决定再开一个帖子,认真描述下这四种情况。
RB-Tree的四种调整情况: http://blog.tk-xiong.com/archives/803
然后接下来,我们来看看
RB-Tree 的结点设计:
RB-Tree拥有,红黑二色,拥有左右子节点,以下是SGI实现源码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
//部分类型定义 typedef bool __rb_tree_color_type const __rb_tree_color_type __rb_tree_red = false; const __rb_tree_color_type __rb_tree_black = true; //红黑树基础结点 struct __rb_tree_node_base { typedef __rb_tree_color_type color_type; typedef __rb_tree_node_base* base_ptr; color_type color; base_ptr parent; base_ptr left; base_ptr right; static base_ptr minimun(base_ptr x) { while(x->left != 0) { x = x->left; } return x; } static base_ptr manimun(base_ptr x) { while(x->right != 0) { x = x->right; } return x; } }; //红黑树的结点 template <class Value> struct __tb_tree_node : public __rb_tree_node_base { typedef __rb_tree_node<Value*> link_type; Value value_field; //节点值 }; |
这里要注意的是,有三个指针,两个子节点,一个父节点。
同时根据Max 和 Min函数可以看出,二叉搜索树得到极值真是太容易!
RB-Tree 的迭代器:
要成功地将RB-Tree实现为一个泛型容器,迭代器的设计是一个关键。
首先要考虑了类别(category),它要具备前进(increment)、后退(decrement)、提领(dereference)、成员访问(member access)等操作。
为了更大的弹性,SGI将 RB-Tree的迭代器设计为两层,这种设计理念和slist类似。
下图便是两层迭代器的示意图,描述了双层节点结构和双层迭代器结构之间的关系。
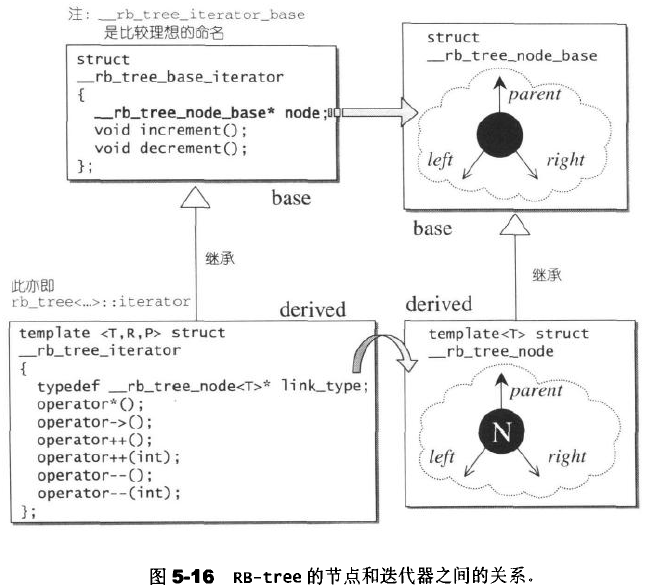
RB-Tree的迭代器属于双向迭代器,但不具备随机定位能力。
基层迭代器实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
struct __rb_tree_base_iterator { typedef __rb_tree_node_base::base_ptr base_ptr; typedef bidirectional_iterator_tag iterator_category; typedef ptrdiff_t difference_type; base_ptr node;//容器指针,和容器产生连结关系 //++的内部实现 void increment() { if(node->right != 0) { //找到右子树的最左边的值 node = node->right; while(node->left != 0) { node = node->left; } } else { //没有右子树 base_ptr y = node->parent; //父节点 while(node == y->right) { //如果是父节点的右子树 //上溯直到不是右子树 node = y; y = y->parent; } //若此时右子节点不等于此时的父节点 if(node->right != y) { //变为父节点... node = y; } //刚开始不理解...试验了一下明白了 } } //--的内部实现 void decrement() { if(node->color == __rb_tree_red && node->parent->parent == node) { //如果是红色节点,且父节点的父节点等于自己,则返回右子节点 node = node->right; //node为header或者end()时... //PS.header的右子节点即为最右边的节点,是最大值 } else if(node->left != 0) { //如果有左子节点 base_ptr y = node->left; while(y->right != 0) { y = y->right; } //左子节点最右边的既是 node = y; } else { //既不是根结点,也不是左子节点 //找到父节点 base_ptr y = node->parent; //一直往上走 while(node == y->left) { node = y; y = y->parent; } //直到不是左子节点 //此时父节点就是我们要找的点... node = y; } //我觉得原理和上面的有点像... } }; |
正式迭代器实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
template <class Value, class Ref, class Ptr> struct __rb_tree_iterator : public : rb_tree_base_iterator { typedef Value value_type; typedef Ref reference; typedef Ptr pointer; typedef __rb_tree_iterator<Value, Value&, Value*> iterator; typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator; typedef __rb_tree_iterator<Value, Ref, Ptr> self; typedef __rb_tree_node<Value>* link_type; __rb_tree_iterator() {} __rb_tree_iterator(link_type x) { node = x; } __rb_tree_iterator(const iterator& it) { node = it.node; } reference operator*() const { return link_type(node)->value_field; } #ifndef __SGI_STL_NO_ARROW_OPERATOR pointer operator->() const { return &(operator*()); } #endif//__SGI_STL_NO_ARROW_OPERATOR self& operator++() { increment(); return *this; } self operator++(int) { self tmp = *this; increment(); return tmp; } self& operator--() { decrement(); return *this; } self operator--(int) { self tmp = *this; decrement(); return tmp; } }; |
以上似乎没什么要注意的…比较好理解。
对于上述的base_iterator 里面比较难以理解的两个++–内部实现…
可以通过以下图来尝试看一下:
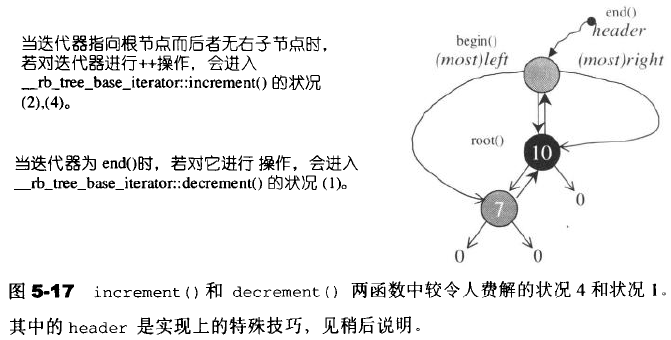
RB-Tree的数据结构:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 |
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc> class rb_tree { protected: typedef void* void_pointer; typedef __rb_tree_node_base* base_ptr; typedef __rb_tree_node<Value> rb_tree_node; typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator; typedef __rb_tree_color_type color_type; public: typedef Key key_type; typedef Value value_type; typedef value_type* pointer; typedef const value_type* const_pointer; typedef value_type& reference; typedef const value_type& const_reference; typedef rb_tree_node* link_type; typedef size_t size_type; typedef ptrdiff_t difference_type; protected: link_type get_node() { return rb_tree_node_allocator::allocate(); } void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); } link_type create_node(const value_type& x) { link_type tmp = get_node(); __STL_TRY{ construct(&tmp->value_field, x); } __STL_UNWIND(put_node(tmp)) return tmp; } link_type clone_node(link_type x) { link_type tmp = create_node(x->value_field); tmp->color = x->color; tmp->left = 0; tmp->right = 0; return tmp; } void destroy_node(link_type p) { destroy(&p->value_field); put_node(p); } protected: //RB-Tree 只以三个数据表现 size_type node_count; link_type header; Compare key_compare; //以下三个函数用来取的header的成员 link_type& root() const { return (link_type&) header->parent; } link_type& leftmost() const { return (link_type&) header->left; } link_type& rightmost() const { return (link_type&) header->right; } //以下6个函数用来取节点x的成员 static link_type& left(link_type x) { return (link_type&)(x->left); } static link_type& right(link_type x) { return (link_type&)(x->right); } static link_type& parent(link_type x) { return (link_type&)(x->parent); } static reference value(link_type x) { return x->value_field; } static const Key& key(link_type x) { return KeyOfValue()(value(x)); } static color_type& color(link_type x) { return (color_type&)(x->color); } //以下六个函数用来取的x的成员 static link_type& left(base_ptr x) { return (link_type&)(x->left); } static link_type& right(base_ptr x) { return (link_type&)(x->right); } static link_type& parent(base_ptr x) { return (link_type&)(x->parent); } static reference value(base_ptr x) { return ((link_type)x)->value_field; } static const Key& key(base_ptr x) { return KeyOfValue()(value(link_type(x))); } static color_type& color(base_ptr x) { return (color_type&)(link_type(x)->color); } //求极大值和极小值 static link_type minimum(link_type x) { return (link_type) __rb_tree_node_base::minimum(x); } static link_type maximum(link_type x) { return (link_type) __rb_tree_node_base::maximum(x); } public: typedef __rb_tree_iterator<value_type, reference, pointer> iterator; private: iteraator __insert(base_ptr x, base_ptr y, const value_type& v); link_type __copy(link_type x, link_type p); void __erase(link_type x); void init() { header = get_node(); color(header) = __rb_tree_red; root() = 0; leftmost() = header; rightmost() = header; } public: rb_tree(const Compare& comp = Compare()) : node_count(0), key_compare(comp) { init(); } ~rb_tree() { clear(); put_node(header); } rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x); public: Compare key_comp() const { return key_compare; } iterator begin() { return leftmost(); } iterator end() { return header; } bool empty() const { return node_count == 0; } size_type size() const { return node_count; } size_type max_size() const { return size_type(-1); } public: //将x插入到RB-Tree中-独一无二 pair<iterator, bool> inser_unique(const value_type& x); //将x插入到RB-Tree中-允许重复 iterator insert_equal(const value_type& x); //... }; |
以上就是RB-Tree的数据结构…可以慢慢理解,我觉得前面看了那么多,现在也该适应了。
RB-Tree的构造与内存管理:
这里构造和析构,空间配置都在前面展示出来了
这里要注意的是init()这个函数的一个实现技巧:
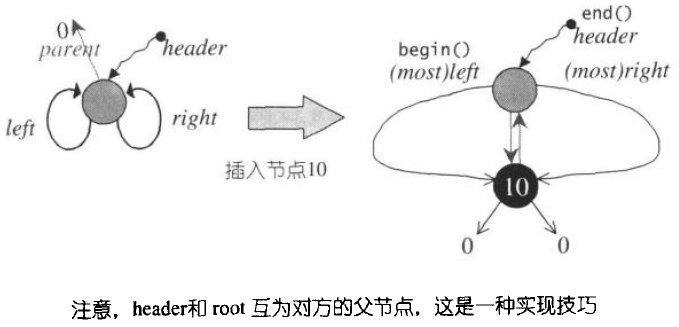
RB-Tree 的元素操作:
这一节主要只谈元素的插入和搜寻。
RB-Tree提供两种插入方式:独一无二的插入和可重复的插入。
首先看看可重复的:insert_equal()
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
template <class Key,class Value, class KeyOfValue, class Compare, class Alloc> typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_equal(const Value &v) { link_type y = header; link_type x = root();//从根结点开始寻找 while(x != 0) { y = x; x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x); } //遇大往左,否则往右... //插入 return __insert(x, y, v); } |
然后是不可重复的:insert_unique() :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc> pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool> rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v) { link_type y = header; link_type x = root(); //从根结点开始 bool comp = true; while(x != 0) { //查找适当的插入点 y = x; comp = key_comp(KeyOfValue()(v), key(x)); x = comp ? left(x) : right(x); } //y即插入节点的父节点 iterator j = iterator(y); if(comp) { //如果离开while循环后comp的值为true(大),则插入到左侧。 //如果插入的父节点是最左边的,则插入 if(j == begin()) { return pair<iterator, bool>(__insert(x, y, v), true); } //否则回头调整 else { --j; } } //如果没有重复 if(key_compare(key(j.node), KeyOfValue()(v))) { return pair<iterator, bool>(__insert(x, y, v), true); } //到这里就肯定是重复了,就不插入了,直接返回。 return pair<iterator, bool>(j, false); } |
然后看一下真正的插入程序 __insert() :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc> typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>:: __insert(base_ptr x_, base_ptr y_, const Value& v) { //参数x_为新值插入点,参数y_为插入点之父节点,参数v为新值 link_type x = (link_type) x_; link_type y = (link_type) y_; link_type z; //key_compare 是键值大小比较标准,是一个 function object if(y == header || x != 0 || key_compare(KeyOfValue()(v),key(y))) { z = create_node(v); //产生一个新结点 left(y) = z; //这使得当y为header时,leftmost = z if(y == header) { //y是header 则表示z是root了 //或者说此时RB-Tree内为空 root() = z; rightmost() == z; } else if(y == leftmost()) //如果y为最左节点 { //维护leftmost,使它一直指向最左节点 leftmost() = z; } } else { z = create_node(v); //创建一个新结点 right(y) = z; if(y == rightmost()) { rightmost() = z; } } parent(z) = y; //设定新结点的父节点 left(z) = 0; //设定新结点的左子节点 right(z) = 0; //设定新结点的右子节点 //设定新结点颜色 - 并调整 //参数分别是 新结点 root __rb_tree_rebalabce(z, header->parent); //结点数量累加 ++node_count; //返回迭代器 return iterator(z); } |
__insert()函数是真正的插入函数…
然后接下来我们看看调整RB-Tree结构和颜色的函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
inline void __rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root) { x->color = red; //新结点默认为红 //如果父节点为红色 while(x != root && x->parent->color == __rb_tree_red) { //如果父节点是祖父节点的左子节点 if(x->parent == x->parent->parent->left) { //令y为伯父节点 - 父节点的兄弟 __rb_tree_node_base* y = x->parent->parent->right; //如果伯父节点存在,并且也是红色 if(y && y->color == __rb_tree_red) { x->parent->color = __rb_tree_black; y->color = __rb_tree_black; x->parent->parent->color = __rb_tree_red; x = x->parent->parent; } //伯父节点不存在,或者伯父节点为黑 else { if(x == x->parent->right) { //如果新结点为父节点之右子节点 x = x->parent; //x为左旋点 __rb_tree_rotate_left(x, root); } //改变颜色 x->parent->color = __rb_tree_black; x->parent->parent->color = __rb_tree_red; //x->parent->parent 为右旋点 __rb_tree_rotate_right(x->parent->parent, root); } } //父节点为祖父节点右子节点 else { //令 y 为伯父节点 __rb_tree_node_base* y = x->parent->parent->left; //伯父节点为红色 if(y && y->color == __rb_tree_red) { x->parent->color = __rb_tree_black; y->color = __rb_tree_black; x->parent->parent->color = __rb_tree_red; x = x->parent->parent; } //无伯父节点 - 或伯父节点为黑 else { //如果新结点为父节点的左子节点 if(x == x->parent->left) { x = x->parent; __rb_tree_rotate_right(x, root); } x->parent->color = __rb_tree_black; x->parent->parent->color = __rb_tree_red; __rb_tree_rotate_left(x->parent->parent, root); } } } //根结点颜色永远为黑色 root->color = __rb_tree_black; } |
这就是那个由上而下的调整程序,也是前面提到的RB-Tree的调整代码。
然后接下来看看RB-Tree左旋和右旋的代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
//左旋 inline void __rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root) { //x为旋转点 __rb_tree_node_base* y = x->right; x->right = y->left; if(y->left != 0) { y->left->parent = x; } y->parent = x->parent; //y顶替x if(x == root) { root = y; } else if(x == x->parent->left) { x->parent->left = y; } else { x->parent->right = y; } y->left = x; x->parent = y; } //右旋 inline void __rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root) { //x为旋转点 //y为旋转点的左子节点 __rb_tree_node_base* y = x->left; x->left = y->right; if(y->right != 0) { y->right->parent = x; } y->parent = x->parent; //令y顶替x if(x == root) { root = y; } else if(x == x->parent->right) { x->parent->right = y; } else { x->parent->left = y; } y->right = x; x->parent = y; } |
这段对照着前面的左旋右旋的情况看吧…
然后扯一下元素的查找…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
//在RBTree中寻找键值为K的结点 template <class Key, class Value, class KeyOfValue, class Compare, class Alloc> typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator tb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) { link_type y = header; link_type x = root(); while(x != 0) { if(!key_copare(key(x),k)) { y = x, x = left(x); } else { x = right(x); } } iterator j = iterator(y); return (j == end() || key_compare(k, key(j.node))) ? end() : j; } |
好了,就这样了…理解了就好。反正我还不懂。
但是大致流程都清楚了。
