昨天比较饿…今天又来更新了一下。
题目只有爬山 和 47幸运数这两题。
第一题:爬山
时间限制:C/C++语言 1000MS;其他语言 3000MS
内存限制:C/C++语言 65536KB;其他语言 589824KB
题目描述:
小B曾经酷爱网络游戏,整日通宵达旦的玩游戏,导致身体素质急剧下降,因此下决心痛改前非,远离一切电子产品,并通过远足爬山的方式改变生活方式并提高身体素质。由于担心对身体造成太大的负荷,他总是选择最平坦的路径,并记录每天的行程情况及达到的最高海拔,使得连续两天之间的海拔之差最多为一个单位。不幸的是,在行程结束时,他不小心掉进河里,造成部分记录信息遗失。他想知道自己行程中可能达到的最高海拔,你是否能够帮忙?
输入
输入有若干组,每组的第一行为空格分隔的两个整数n和m,1<=n<=10^8, 1<=m<=10^5,分别表示行程天数以及未遗失的记录数。随后紧跟m行,每行为空格分隔的两个整数d和h,1<=d<=n, 0<=h<=10^8,表示行程的第几天及当天达到的最高海拔。
输出
对每组输入,如果记录是可能的,则在单独的行中输出可能达到的最高海拔,否则输出字符串“IMPOSSIBLE”(不含引号)。
样例输入
8 2
2 0
7 0
8 3
2 0
7 0
8 3
样例输出
2
IMPOSSIBLE
Hint
第一天和最后一天的海拔可以是任何值。
题目的意思比较明确,就是小B从网络游戏转行爬山了,但是体力不好,每天只能上一个单位,或者下一个单位,或者不上不下 (假设不是上两个下一个这样的),然后问他最高能到啥位置。
我们看第一组样例:
| 天号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 最大值1 | 1 | 0 | 1 | 2 | 2 | 1 | 0 | 1 |
| 最大值2 | 1 | 0 | 1 | 1 | 2 | 1 | 0 | 1 |
这是可能的情况,其他还有很多都不列举了。
然后我直接说解法:
核心代码就是:
|
1 2 3 4 |
map <int,int> vi; vector <int> v; int temp = (v[i] - v[i-1])/2 + (vi[ v[i] ] + vi[ v[i-1] ])/2; |
这里的vi 是 <天,高度>
这里的 v是哪一天的号码。
求出来的temp 是 2 0 和 7 0 它们之间能够达到的最大高度。
即 : (7-2)/2 + (h(7) – h(2))/2 – 即两天相差的天数 和 他们的高度 与最大值的关系。
这里要注意的是… 还得考虑到 2 – 1 和 7 – 0 这样的情况。
这种情况下 我的 公式计算出来的是 2 ,但是实际情况是这样的:
| 天号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 高度 | 1 | 2 | 3 | 2 | 1 | 0 |
所以最大值实际是3…但是因为AC代码是这样的。所以不太敢乱改了。
更新公式:
|
1 |
int temp = (v[i] - v[i-1] + vi[ v[i] ] + vi[ v[i-1] ])/2; |
这样对数据 2-1 7-0 计算出来就是 (7 – 2 + 1 + 0) /2 = 3.
因为我提交的时候,前面可能错误的方法AC了,所以就没有管了,具体用哪个公式…我觉得第二个对。
可能还是题目给的例子不全吧…
然后怎么判断Impossible 就是给出的两个数据的高度差值大于天数间距,这种情况下无论如何都不可能达到恰好每天增长或减少1的。嗯…大致就是这个思路
然后注意还要判断首和尾…即从第一天开始 到 给出的第一个数据之间,还有从给出的最后一个数据到最后一天。
代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
/* Author : xiong */ #include <stdio.h> #include <string.h> #include <math.h> #include <stdlib.h> #include <memory.h> #include <time.h> #include <limits.h> #include <iostream> #include <iomanip> #include <cstdlib> #include <cstdio> #include <cstring> #include <string> #include <cmath> #include <algorithm> #include <cassert> #include <climits> #include <ctime> #include <vector> #include <queue> #include <list> #include <stack> #include <map> #include <numeric> #include <sstream> #include <set> #include <utility> #include <deque> #include <functional> #include <iterator> #define CASET int ___T, case_n = 1; scanf("%d ", &___T); while (___T-- > 0) #define MST(X,T) memset((X), (T), sizeof((X))) #define LEN(X) strlen(X) using namespace std; const int MOD = 1e9+7; const int N_SIZE = 1e6+10; map <int,int> vi; //存储天数 - 高度 vector <int> v; //存储天数 int main() { int n, m; //这个Flag是快速返回的 - goto backFlag: while(cin >> n >> m) { v.clear(); vi.clear(); int d,h; //输入数据 for(int i=0;i<m;i++) { cin >> d >> h; vi[d] = h; v.push_back(d); } //把输入的天数 排序一下。 sort(v.begin(),v.end()); //首先处理第一个数据 到 第一天 这个最大值。 int Max = vi[ v[0] ] + v[0]-1; //然后处理两两数据之间的高度 比如 2-0 和 7-0 这样的 for(int i = 1; i < v.size(); i++) { //如果两个数据之间的高度差大于天数了,是无论如何都无法达到的 if(abs(vi[ v[i] ] - vi[ v[i-1] ]) > v[i] - v[i-1]) { cout << "IMPOSSIBLE" << endl; goto backFlag; } //否则计算出这两天之间能达到的最大值,然后与前面的最大值判断 else { int temp = (v[i] - v[i-1])/2 + (vi[ v[i] ] + vi[ v[i-1] ])/2; if(temp > Max) Max = temp; } } //最后再处理以下最后一天的值 int temp = vi[ v[m-1] ] + (n - v[m-1]); if( temp > Max ) { Max = temp; } //输出最大值。 cout << Max << endl; } } |
第二题幸运数:
时间限制:C/C++语言 1000MS;其他语言 3000MS
内存限制:C/C++语言 65536KB;其他语言 589824KB
题目描述:
4和7是两个幸运数字,我们定义,十进制表示中,每一位只有4和7两个数的正整数都是幸运数字。前几个幸运数字是:4,7,44,47,74,77,444,447…
现在输入一个数字k,输出第k个幸运数
输入输出我忘了。
样例输入
3
5
100
10000000
样例输出
74
744747
44774447447477474444447
这题目就是格雷码…
代码如下: 注意一定是Long Long – 我调了20分钟,就是因为它。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
/* Author : xiong */ #include <stdio.h> typedef long long LL; void Lucky(LL n) { if(n <= 0)return ; LL Prev = (n-1)/2; LL Now = n - Prev*2; if(n == 1){ printf("4"); return ; } else if(n == 2){ printf("7"); return ; } else { if(Prev > 0) Lucky(Prev); if(Now > 0) Lucky(Now); } } int main() { LL T; scanf("%lld",&T); while(T--) { LL n; scanf("%lld",&n); Lucky(n); puts(""); } } |
PS.幸运数我下来略微改动了一下,不过肯定可以AC的。
有人问思想,我来补充下。打表: 0 是 NULL
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 4 | 7 | 44 | 47 | 74 | 77 | 444 | 447 | 474 | 477 |
我们可以看到
Lucky(3) 是 Lucky(1) + 4
Lucky(4) 是 Lucky(1) + 7
Lucky(5) 是 Lucky(2) + 4
Lycky(6) 是 Lucky(2) + 7
是不是和格雷码的 0 1 00 01 10 11 … 很像。
画个图哈

这样就很清楚了…
我要输出444 就输出 44 (Lucky(Prev)) 然后输出一个 4 (Lucky(Now))
我要输出 744 就输出一个 74 然后输出一个 4
好理解吧…
有网友简化了一下Lucky函数…这里贴一下:我还是稍微改了下…那些中间值不用也罢。
但是就是可能写上,清楚一些。 447 可以理解为 44是前一层, 7 是当前层。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
void Lucky(LL n) { if(n <= 0)return ; //先输出前面的数据 int Prev = (n-1)/2; Lucky(Prev); //然后输出当前层的数据 LL Now = n % 2; Now == 0 ? printf("7") : printf("4"); } |
然后根据网友的建议…再画一个二叉树的图…帮助理解:
按这个思路来:每一条路径就是一个结果…
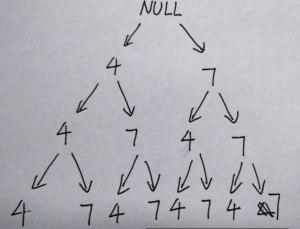
这里网友提供了一种新方法:二进制方法 – 打表如下:
| 输入数据 | 二进制数据 | 处理分析 | 最终结果 |
| 1 | 1 | 不输出 | NULL |
| 2 | 10 | 0 | 4 |
| 3 | 11 | 1 | 7 |
| 4 | 100 | 00 | 44 |
| 5 | 101 | 01 | 47 |
| 6 | 110 | 10 | 74 |
| 7 | 111 | 11 | 77 |
| 8 | 1000 | 000 | 444 |
| 9 | 1001 | 001 | 447 |
| 10 | 1010 | 010 | 474 |
…后面就省略了-理论上完全可行的,略去了递归的层数。 代码如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
void Lucky(LL n) { //首先做 +1 处理 n+=1; if(n <= 1)return ; char Str[20]; int idx = 0; //计算最后一位(这样是倒着计算的) - 注意当处理到1的时候表示结束 while(n > 1) { n&1 ? Str[idx++] = '7' : Str[idx++] = '4'; n = n>>1; } //所以输出的时候也倒着输出 for(int i = idx-1; i >= 0; i-- ) { printf("%c",Str[i]); } } |
以上代码都理论AC 。可以随意取用。转载请注明来源。

楼主好6啊,我只想问拿了几个offer
第三个幸运数字应该是44啊?楼主
你说的是输入样例吗?那个3表示有三组数据。